بخشی از مقاله
*** این فایل شامل تعدادی فرمول می باشد و در سایت قابل نمایش نیست ***
بهبود الگوریتم خوشه بندی K-means با استفاده از الگوریتم پیشنهادی فاخته توسعه یافته
چکیده
امروزه، خوشهبندی نقش مهمی را در اغلب زمینههای تحقیقاتی مانند مهندسی، پزشکی، زیست شناسی، داده کاوی و... ایفا مینمایـد. یکـی از الگـوریتمهـای معروف خوشهبندی، الگوریتم k-means میباشد، این الگوریتم در کنار مزایایی چون سرعت بالا و سهولت پیاده سازی، در دام بهینه محلی قرار گرفته و همواره جواب بهینه مساله را تولید نمی کند. به همین دلیل ما در این مقاله سعی نموده ایم با تعیین مراکز بهینه اولیه خوشه ها برای الگوریتم k-means، با اسـتفاده از الگوریتم پیشنهادی فاخته توسعهیافته، تا درصد بالایی نتایج خوشهبندی را از بهینه محلی خارج نموده و به بهینه سراسری نزدیک نماییم. الگوریتم پیشنهادی، توسعهیافته الگوریتم فاخته کلاسیک می باشد که ما در روش پیشنهادی خود، تعدادی از عملگرهای آن را هدفمند و متنوع نموده ایم، بطور نمونه جهت افزایش سرعت همگرایی الگوریتم پیشنهادی، سعی نمودهایم جمعیت اولیه با پراکندگی بیشتر در فضای مساله، با استفاده از توالی آشوب تولید نماییم، همچنین جهت افزایش دقت و سرعت همگرایی الگوریتم، روال تعیین تعداد تخم برای هر فاخته موجود در جمعیت، مبتنی بر میزان شایستگی آن فاخته میباشد، در بهبودی دیگر جهت افزایش پوشش سراسری در فضای مساله، دستههای فاخته ایجاد شده حاصل از مرحله خوشه بندی فاختهها را با درجه انحراف متفاوت در محـیط به سمت فاخته بهینه سراسری مهاجرت خواهیم داد.
سپس به منظور اعتبارسنجی، روش پیشنهادی بر روی چندین مجموعه داده اسـتاندارد از سـایت UCI مـورد ارزیـابی قـرار گرفتـه اسـت و نتـایج حاصـل بـا الگوریتمهای چاله سیاه، الگوریتم مبتنی بر تئوری انبساط؛ انقباض، الگوریتم جستجوی فاخته (یانگ)، الگوریتم بهینه سازی فاخته (رجبیون) و الگـوریتم k-means از لحاظ شاخصهای؛ دقت، سرعت همگرایی و پایداری جواب ها مقایسه شده است. بررسی نتایج نشان میدهد، الگوریتم جدید ما قادر است جـواب بهینه نهایی را با دقت، پایداری و سرعت همگرایی بالا در مقایسه با الگوریتمهای دیگر تولید نماید.
کلمات کلیدی: خوشه بندی، داده کاوی، الگوریتم k-means، الگوریتم فاخته توسعه یافته
-1 مقدمه
خوشــهبنــدی یکــی از مشــهورترین تکنیــک هــای داده کــاوی مــی باشــد. خوشه بندی، فرآیندی است که در آن داده ها در گروههای مجزا قرار می گیرند بطوریکه داده ها در هـر گـروه یـا خوشـه بیشـترین شـباهت را بـا یکـدیگر و بیشترین تفاوت را با دادههای دیگر گروهها یا خوشه ها دارنـد.[1] از آنجـا کـه خوشه بندی یک روش یـادگیری بـدون نـاظر محسـوب مـیگـردد، در مـوارد بســیاری همچــون؛ علــوم مهندســی، علــوم پزشــکی، علــوم اجتمــاعی، علــوم زمینشناسی، پردازش تصویر و...کاربرد دارد.[2] الگوریتم خوشه بندی افـرازی به دلیل پیچیدگی محاسباتی بسیار پایین، به ویژه در مجموعه دادههای بزرگ یکی از رایجترین الگوریتم های خوشه بندی می باشـد، در ایـن الگـوریتم N داده به K خوشه با سرعت بالا تقسیم می گردد، بطوریکه نمونه ها در هر افـراز بیشترین شباهت را با یکدیگر و بیشترین تفاوت را با نمونهها در خوشه های دیگر دارند. یکی از الگوریتمهای خوشهبنـدی افـرازی مشـهور در ایـن زمینـه الگوریتم k-means می باشد، این الگوریتم در سال 1967 توسط Macqueen و همکارانش مطرح شد[3] ؛ و بعد از حدود 4 دهه از ابـداع آن همچنـان ایـن الگوریتم از الگـوریتم هـای محبـوب خوشـهبنـدی مرکـز- محـور در تکنیـک خوشهبندی میباشد. این الگوریتم در کنار مزایایی چون سهولت پیادهسـازی، سرعت عملکرد بالا و مقیاس پذیر بـودن در مجموعـه دادههـای بـزرگ[3,4]، دارای معایبی همچون وابسته بودن نتایج الگوریتم به شرایط اولیـه آن، ماننـد مراکز اولیه خوشه ها می باشد که گاه باعث می شود به دلیل انتخـاب نامناسـب آن ها، پاسخ نهایی الگوریتم در دام بهینه محلی قرار گیرد و دقت خوشهبنـدی کاهش یابد، لذا تضمینی برای رسیدن به جواب مـورد انتظـار وجـود نخواهـد داشت. در چند دهه اخیر راهکارهای متفـاوتی در جهـت بهبـود چـالش قـرار گــرفتن نتــایج الگــوریتم k-means در دام بهینــه محلــی بــا اســتفاده از الگوریتم های تکاملی مطرح شده است، بطورکلی در این راهکارها سـعی شـده است با استفاده از الگوریتم های تکاملی به طور مستقل یا ترکیب بـا الگـوریتم k-means تا حدود زیادی نتایج الگـوریتم خوشـه بنـدی از دام بهینـه محلـی خارج گـردد. بـه طـور مثـال، راهکارهـایی مبتنـی بـر؛ -1 الگـوریتم ژنتیـک Mualik) و همکــــارانش،[5] (2000،-2 جســــتجوی ممنوعــــه sung) و همکارانش،[6] (2000، -3الگوریتم کلونی مورچگان Shelokar) و همکارانش، [7](2004، -4 جفت گیری زنبورعسـل Fathian) و همکـارانش-[8] (2007، -5 الگوریتم ژنتیک Laszlo) و همکارانش-[9] (2007، -6 ترکیب پیونـدی از الگوریتم های کلـونیمورچگـان و سـرد شـدن شـبیه سـازی شـده (نیکنـام و همکـارانش - [10] (2007، -7 ترکیـب پیونــدی از الگـوریتم بهینــه ســازی انبوهذرات و سردشدن شبیه سازی شده (نیکنام و همکارانش - [11] (2007، -8 ترکیب ترتیبی الگـوریتم بهینـه سـازی انبـوه ذرات و Rana) k-means و همکــارانش - [12] (2010،-9 ترکیــب الگــوریتم بهینــه ســازی انبــوه ذرات، الگوریتم سرد شدن شبیه سـازی شـده و ) k-means بهمنـی و همکـارانش - [13] (2010،-10 ترکیــب الگــوریتم بهینــهســازی انبــوه ذرات، الگــوریتم کلونیمورچگان و k-means (نیکنام و همکارانش - [14](2010، -11 ترکیـب الگوریتم رقابت استعماری توسـعهیافتـه و k-means (نیکنـام و همکـارانش - [15] (2010، -12 مفهـوم تئـوری انبسـاط- انقبـاض (حـاتملو-[16](2011 ، -13 مفهــوم تئــوری چالــه ســیاه (حــاتملو-[17](2013، -14 جســتجوی فاخته(Manikandan و همکارانش-.[18] (2014
به طور کلی الگوریتمهای تکاملی که تاکنون مطرح شده اند را میتوان به دو دسته تقسیم نمود؛ دسته اول؛ الگـوریتم هـای تکـاملی بـا ماهیـت جسـتجوی سراسری مانند؛ PSO1,ACO2,GA3 و دسته دوم؛ الگوریتم هـای تکـاملی بـا ماهیت جستجوی محلی مانند .SA4,TS5 الگوریتم های دسـته اول بـه دلیـل جستجوی سراسری در فضای مساله احتمال قـرار گـرفتن نتـایج آنهـا در دام بهینه محلی کمتر از دسته دوم می باشد اما به دلیل عـدم جسـتجوی محلـی، پاسخ های نهایی در این دسته دارای دقت کمتری میباشد، دسته دوم به دلیل عدم جستجوی سراسری در فضای مساله احتمال قرار گرفتن نتایج آنها در دام بهینه محلی بیشتر از دسته اول میباشد، اما در این دسته به دلیل جسـتجوی محلی، در جهت افزایش دقت پاسـخهـای نهـایی، تـلاش بیشـتری مـیشـود. معمولاً محققان برای پوشش نقاط ضعف هر یک از دسته های فوق، آنها را بـا یکدیگر ترکیب می نمایند که این ترکیب خود باعث افزایش دقـت پاسـخهـای نهایی و به تبع آن افزایش پیچیدگی محاسباتی الگوریتم ترکیبی خواهد شد.
در ادامه، الگوریتم تکاملی فاخته مطرح و سپس توسعه داده خواهد شد که به طور همزمان جستجوی محلی و سراسری در ماهیت این الگـوریتم قـرار دارد. الگوریتم بهینهسازی فاخته(COA)6، الگوریتم تکاملی جدیدی می باشد که در ســال 2011 توســط رامــین رجبیــون بــرای حــل بســیاری از انــواع مســائل بهینهسازی مطرح گردید[19]، در این الگوریتم که الهام گرفته از زندگی پرنده فاخته می باشد عملگرهایی در نظر گرفته شده است کـه قـادر بـه جسـتجوی محلی و سراسری در فضای مساله به طور همزمـان مـی باشـد، بنـابراین ایـن الگوریتم قادر است به نتایج بهینه نهایی با دقت بالا و سرعت همگرایی سـریع دست یابد، اما این الگوریتم دارای معایبی می باشد که ما سـعی نمـودهایـم در روش پیشنهادی خود که توسعهیافته الگوریتم فاخته کلاسیک می باشـد و مـا آن را ECOA7 نامیدهایم، این مشکلات را اصلاح نموده و برای افزایشکـارایی الگوریتم تعدادی از عملگرهای آن را هدفمنـد نمـاییم. الگـوریتم پیشـنهادی فاخته توسعهیافته دارای کارایی بالاتر از الگوریتم فاخته کلاسیک میباشد.
برای اندازه گیری کیفیت خوشهبندی توابع برازنـدگی مختلفـی تعریـف شـده است کـه یکـی از مهمتـرین و پراسـتفادهتـرین آنهـا میـانگین مربـع خطاهـا می باشد. مقدار تابع برازندگی برای مسئله خوشـهبنـدی در ایـن مقالـه برابـر میانگین فاصله دادهها از مراکز خوشه ها میباشد و بـا اسـتفاده از معادلـه (1) تعریف می شود:
بطوریکه hi={h1 , h2,…, hk} نشاندهنـده فاختـه i ام اسـت کـه شـامل k مرکز خوشه می باشـد وhim نمایـانگر مرکـز خوشـه m ام از فاختـه iم اسـت. همچنین xj={x1 , x2,…,xN} و N تعداد کـل دادههـا مـی باشـد. در ایـن مقاله برای محاسبه فاصله نمونهها تا مراکز خوشه ها از فاصله اقلیدسی استفاده شده است. مقدار مطلوب برای تابع برازندگی فوق مقدار حداقل می باشد.
در ادامه مقاله، در بخش2 مروری بر الگوریتم فاخته کلاسیک خواهیم داشـت. سپس در بخش3 ، الگوریتم پیشنهادی فاخته توسعهیافته مطرح خواهـد شـد. در بخش4، نتایج بدست آمده از شبیه سازی الگوریتم پیشنهادی بر روی چند مجموعه داده نشان داده می شود و در نهایت در بخش 5، نتیجـهگیـری ارائـه شده است.
-2 الگوریتم فاخته کلاسیک
این الگوریتم بهینه سازی، از زندگی یک خانواده از پرندگان به نام فاختهها، الهــام گرفتــه اســت. زنــدگی خــاص ایــن نــوع پرنــده و ویژگــیهــای آن در تخمگذاری و زاد و ولد، انگیزه اصلی پرورش این الگوریتم تکاملی بهینهسازی جدید بوده است. در ادامه روال کلی در الگوریتم فاخته کلاسیک بیان خواهد شد.
- 1 -2 روال الگوریتم فاخته کلاسیک
-1 تولید جمعیت اولیه فاختهها بصورت تصادفی.
-2 تخصیص تعداد تصادفی تخم به هر فاخته موجود در جمعیت.
-3 تعیین شعاع تخمگذاری فاختهها با استفاده از رابطه (2)
در این رابطه varhi و varlow به ترتیـب حـد بـالا و حـد پـایین متغییرهـا در مسئله بهینه سازی می باشند و α متغیری است که حداکثر مقدار ELR بـا آن تنظیم میشود.
-4 تخمگذاری فاختههـا در شـعاع تعیـین شـده و سـپس محاسـبه میـزان شایستگی تمام تخمها در محیط.
-5 انتخاب تعداد حداکثر فاختههایی که در هر دور میتوانند زنده بمانند. -6 خوشهبندی فاختههای موجود در محیط و سـپس بـه روزرسـانی فاختـه بهینه سراسری.
-7 مهاجرت همه دسته فاختهها به سمت فاخته بهینه سراسـری و بازگشـت به گام 2 تا رسیدن به شرط خاتمه الگوریتم.
در نهایت فاخته بهینه سراسری به عنوان راه حل بهینه نهایی اعلام میشود.
-3 الگوریتم پیشنهادی فاخته توسعه یافته
در الگوریتم فاخته توسعهیافته جهت افزایش کـارایی الگـوریتم نسـبت بـه نسخه اولیه آن، تعدادی از عملگرهای آن را اصلاح و هدفمند نمودهایم که در ادامه این تغییرات با جزئیات تشریح میشود.
-1-3 تولید جمعیت اولیه مبتنی بر توالی آشوب
نسخه اولیه الگوریتم فاخته از توالیهای تصادفی برای تولید جمعیـت اولیـه استفاده میکند، استفاده از پارامترهای تصادفی در الگوریتم بهینهسازی فاخته ممکن است کارایی الگوریتم را تحت تأثیر قرار دهد و نتواند پوشش سراسـری به کل فضای جستجو را تـامین کنـد، در نتیجـه سـرعت همگرایـی الگـوریتم کاهش می یابد و دقت پاسخهانسبتاً کم خواهد شد. در الگوریتم پیشنهادی به منظور افزایش پراکندگی جمعیت اولیـه فاختـه هـا اسـتفاده از تـوالی آشـوب جایگزین استفاده از توالی تصادفی در تولید جمعیت اولیه خواهد شـد، بـدین ترتیب جمعیت اولیه تولید شده با استفاده از توالی آشوب دارای پراکنـدگی و تنوع بیشتر در فضای مساله می باشند کـه در نهایـت باعـث افـزایش سـرعت همگرایی الگوریتم به پاسخ بهینه نهایی خواهد شد. نقشه آشوبی که توالی های آشوب را در این مقاله تولید میکند Logistic Map است که در سـال 1976 توسط Robert May مطرح شد .[20,21]
این نگاشت با استفاده از رابطه (3) تعریف میشود:
بطوریکه λ مقدار اولیه تابع و xn مقدار تابع بعد از n مرتبـه تکـرار مـیباشـد. وابستگی رفتار تابع به متغیرλبستگی دارد و معمولاً مقدار 4 انتخاب می شود. در رابطه (4) به فرمول تولید جمعیت اولیه مبتنی بر استفاده از توالی تصادفی در نسخه اولیه الگوریتم فاخته اشاره دارد.
رابطه (5) به تولید جمعیت اولیه مبتنی بر استفاده از توالی آشوب در الگوریتم ECOA اشاره مینماید.
در رابطه فوق، Cr توالی آشوب را تولید می کنـد کـه در رابطـه (3) بـه نحـوه محاسبه آن اشاره شده است.
-2-3 تخم گذاری هدفمند
در الگوریتم فاخته کلاسیک نحوه تعیین تعداد تخم برای هر فاخته موجـود در جمعیت، تصادفی میباشد و سپس شعاع تخمگذاری فاختـههـا، بـراسـاس تعداد تخم تصادفی هر فاخته تعیین میشود. استفاده از توالی تصـادفی بـرای تعیین تعداد تخم، سرعت همگرایی و دقت الگوریتم را کـاهش مـیدهـد زیـرا ممکن است در مواردی به دلیل سیاست تصادفی به فاخته ای که در موقعیـت بهتر از فاختههای دیگر در فضای مسئله قرار دارد، تعداد تخم کمتر و بالعکس به فاخته در موقعیت نامناسب در فضای مسئله، به طور تصـادفی تعـداد تخـم بیشتری تخصیص یابد، بنابراین در مواردی، موقعیت نامناسب در فضای مساله بیشتر از موقعیت مناسب، کاوش و بررسی خواهـد شـد، بـدین ترتیـب باعـث کاهش سرعت همگرایی و دقت الگوریتم فاخته کلاسیک در رسیدن به پاسـخ نهایی می شود. در روش پیشنهادی، تعداد تخم تخصیص یافته بـه هـر فاختـه متناسب با میزان شایستگی آن فاخته می باشد کـه بـا اسـتفاده از رابطـه (6) محاسبه میشود.
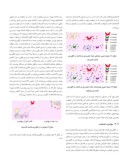
در این رابطه Eggi تعداد تخم تخصیص یافته به فاختـه iام، minegg تعـداد حداقل تخم، fitnessi میزان شایستگی فاخته i ام، minfit مقدار حداقل تـابع شایستگی فاختههای موجود، maxegg تعداد حداکثر تخمها و maxfit مقدار حداکثر تابع شایستگی فاختهها موجود در فضای مسئله می باشد. با استفاده از این رابطه تعداد تخم تخصیص یافته به هر فاخته هدفمند و با توجه به مقـدار fitness هر فاخته می باشد که باعث افزایش دقت و سرعت همگرایی الگوریتم به پاسخ بهینه نهایی خواهد شد. در تصویر شماره (1) نتیجه تعیـین تصـادفی تعداد تخم برای هر فاخته در الگوریتم فاخته کلاسیک و در تصویر شـماره((2 نتیجــه تعیــین هوشــمندانه تعــداد تخــم بــرای هــر فاختــه در الگــوریتم فاختهتوسعهیافته نشان داده شده است. در ایـن تصـاویر فاختـه هـا بـا انـدازه بزرگتر، فاختههایی هستند که در موقعیت بهتر در فضای مسئله قرار دارند و فاختهها با اندازه کوچک تر فاختهها در موقعیـت نامناسـب در فضـای مسـئله میباشند.
شکل :(1) نتیجه تعیین تصادفی تعداد تخم برای هر فاخته در الگوریتم فاخته کلاسیک
شکل(:(2 نتیجه تعیین هوشمندانه تعداد تخم برای هر فاخته در الگوریتم فاخته توسعهیافته
همان طور که در تصـاویر مشـاهده نمودیـد، در تصـویر شـماره (1) بـه علـت تخصیص تصادفی تعداد تخم به فاختهها، ممکن است فاختهای که در موقعیت مناسب در فضای مساله قرار دارد، بـه طـور تصـادفی تعـداد تخـم کمتـری و بالعکس به فاخته در موقعیت نامناسب تعداد تخم بیشتری تخصیص یابـد کـه در نهایت باعث کند شدن سرعت همگرایـی الگـوریتم در رسـیدن بـه پاسـخ بهینهنهایی خواهد شد که ایـن مسـئله در الگـوریتم توسـعه یافتـه فاختـه بـا تخصیص هوشمندانه تعداد تخم به هر فاخته رفع شده است.
-3-3 مهاجرت هدفمند
در الگوریتم فاخته کلاسیک بعـد از مرحلـه خوشـهبنـدی فاختـههـا، تمـام دستهها با یک درجه انحراف یکسان به سمت فاخته بهینه سراسری مهـاجرت می نمایند. در الگوریتم فاخته توسعهیافته، بعد از عمل خوشهبندی، دستههای متفاوتی از فاختهها تولید میشوندکه آماده مهاجرت مـی باشـند، در الگـوریتم پیشنهادی، جهت افـزایش پوشـش سراسـری در فضـای مسـاله، دسـتههـای متفاوت از فاختهها با درجه انحراف متفاوت در محیط به سمت فاختـه بهینـه سراسری مهاجرت می نمایند، بطوریکه فقط یک دسته با انحراف بسیار کم بـه سمت فاخته بهینه سراسری مهاجرت کرده تـا در آن منطقـه بـه جسـتجوی فاختههای بهینه با شایستگی بیشتر از فاخته بهینه سراسری جاری بپردازند و مابقی دسـتههـا بـا درجـه انحـراف متفـاوت در فضـا بـه جسـتجو سراسـری می پردازند. زیرا با توجه به ماهیت الگوریتم فاخته که خاصـیت تولیـد مثـل و تکثیر دارد، با یک دسته مهاجرت داده شده در اطراف فاخته بهینه سراسـری بعد از تخمگذاری تعداد زیادی تخم و فاخته ایجاد میشوند که مـیتواننـد آن محیط را بررسی نمایند به عبارتی به اندازه کافی، فاختهها آن محیط را جهت جستجو پوشش خواهند داد. مهاجرت همه دسته فاخته ها در الگوریتم فاختـه اولیه به سمت یک منطقه باعث تراکم بیش از حد فاختـه هـا در یـک منطقـه شده، در نهایت پوشش سراسری فضای مساله کمتر تامین خواهد شـد و اگـر فاختهای در فضای مساله با شایستگی بیشتر از فاخته بهینه سراسری موجود، وجود داشته باشد که به هر دلیلی در مسئله پیدا نشده است، با روش الگوریتم فاخته اولیه احتمال رسیدن به آن فاخته بهینه سراسری واقعی بسیار کـاهش می یابد، بـدین منظـور در روش پیشـنهادی، سـعی شـده اسـت بـا مهـاجرت دستههای مختلف فاخته ها به سمت مناطق مختلف این مشـکل پوشـش داده شــود. در ادامــه عملگــر مهــاجرت در دو روش الگــوریتم فاختــه کلاســیک و فاختهتوسعه یافته بصورت بصـری نشـان داده شـده اسـت.همان طـور کـه در تصویر (3) قسمت ( الف) مشاهده مینمایید در الگوریتم فاخته کلاسیک بعد از مرحله خوشهبندی، همه دسته ها با یک درجه انحراف یکسان به سمت فاختـه بهینه سراسری مهاجرت می نمایند که در تصویر (3) قسـمت (ب) نشـان داده شده است بعد از مهاجرت باعث متمایل شدن همه فاختهها در یـک محـدوده می شود، حال اگر در مساله فاختـه بهینـه سراسـری بهتـری از فاختـه بهینـه سراسری فعلی وجود داشته باشد، شانس پیدا کردن آن بسیار کاهش مییابـد زیرا همه فاختهها به کاوش و بررسی در یک محدوده میپردازند.
در شکل 4 نحوه مهاجرت در الگوریتم فاخته توسـعه یافتـه نشـان داده شـده است.