بخشی از پاورپوینت
اسلاید 1 :
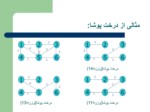
درخت پوشا
درختT درخت پوشای گراف Gاست اگرT زیرگرافG باشد که حاوی تمامی رئوس G است.
درخت پوشا را می توان با استفاده از BFSو DFS بدست آورد…
یکی از خواص جالب درخت پوشا: درخت پوشا کوچک ترین زیرگراف است...
اسلاید 2 :
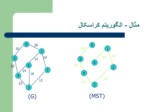
درخت پوشای مینیمم
تعريف1:منظورازهزینه درخت پوشاي يك گراف بدون جهت وزن دار،مجموع هزينه (وزن)هاي يال هاي درخت پوشا است.
تعريف2: درخت پوشا با كمترين هزينه ،درخت پوشايي است كه كمترين هزينه را دارد.
3 الگوريتم براي بدست آوردن MSTوجود دارد.
–الگوریتم کراسکال
–الگوریتم پریم
–الگوریتم سالین
اسلاید 3 :
درخت پوشای مینیمم- ادامه
براي ايجاد درخت پوشا با كمترين هزينه از معیار كمترين هزينه استفاده مي كنيم:
راه حل مطلوب تحت شرايط زير حاصل مي شود:
1.تنها بايد از يال هاي گراف استفاده كند.
2.تنها بايد دقيقا از n-1يال استفاده كند.
3.از يال هايي كه دور ايجاد مي كنند نمي توانداستفاده كند.
اسلاید 4 :
الگوریتم کراسکال
اين الگوريتم با اضافه كردن يال ها به صورت مرحله به مرحله بهT،درخت پوشا با كمترين هزينه ي T را توليد مي كند.
يال ها به ترتيب غير نزولي انتخاب مي شوند.
يك يال بهTاضافه مي شود مشروط بر اينكه با يال هاي اضافه شده قبلي دور تشكيل ندهد.
گرافGهمبند است وn>0راس دارد پس دقيقا n-1 يال براي اضافه شدن در Tانتخاب ميشود.
اسلاید 5 :
الگوریتم کراسکال
E مجموعه اي از يال هاي گراف Gاست.عملياتي كه ميخواهيم انجام بدهيم:
1.تعيين يك يال با كمترين هزينه ( ine 3)
2.حذف اين يال( ine 4)
اسلاید 6 :
قضيه الگوریتم کراسکال
اگر Gيك گراف همبند بدون جهت باشد آنگاه الگوريتم كراسكال، يك درخت پوشا با كمترين هزينه توليد مي كند.
اثبات:
–الف- در صورت وجود يك درخت پوشا،روش كراسكال يك درخت پوشا توليد مي كند.
–ب- درخت پوشاي توليد شده كمترين هزينه را دارد.
اثبات...
اسلاید 7 :
الگوریتم پريم
الگوريتم پريم مانند الگوريتم كراسكالMSTرا تشكيل ميدهد.
در تمام مراحل الگوريتم پريم،مجموعه يال هاي انتخاب شده درخت تشكيل ميدهد
...و لي در كراسكال در هر مرحله جنگل توليد مي شود.
اسلاید 8 :
الگوریتم پريم – پياده سازي
برای هر راس داریم:
–kv :آیا v دیده شده است
–dv :کمترین وزن برای راس v کدام است
–pv :کدام راس ابتدا قرار می گیرد؟
اسلاید 9 :
الگوریتم پريم – پياده سازي
//Assume that G has at east one vertex.
TV={0};//start with vertex 0 and no edges
For (T=nu ; contains fewer than n-1 edges; add (u, v) to T)
{
et (u, v) be a east-cost edge such that u Î TV and v Î TV;
If (there is no such edge) break;
Add v to TV;
If (T contains fewer than n-1 edges) cout <<“no spanning tree”<< end ;
اسلاید 10 :
الگوریتم سالین
الگوریتم سالین در هر مرحله چند یال مختلف را انتخاب میکند.
در آغاز هر مرحله ،یال های انتخاب شده با تمامn راس،یک جنگل پوشا راتشکیل میدهد.
در شروع مرحله اول،مجموعه یالهای انتخاب شده تهی است.
الگوریتم وقتی تمام میشود که تنها یکه درخت تولید شده باشد.