بخشی از مقاله
*** این فایل شامل تعدادی فرمول می باشد و در سایت قابل نمایش نیست ***
تحليل ديناميکي اندرکنش شمع - خاک روانگرا - سازه
خلاصه
با توجه به اينکه مطالعات بارهاي لرزه اي بر روي شمع ها و همچنين پديدة روانگرايي در چهار دهة اخير انجام گرديده اند، ليکن مطالعه ترکيب اين دو، يعني رفتار لرزه اي شمع ها در خاک روانگرا، بشدت احساس مي گردد. با توجه به روند مطالعات به سمت اندرکنش شمع - خاک - سازه، بررسي تأثير روانگرايي بر روي شمع بايد با در نظر گرفتن روسازه صورت گيرد.
در اين تحقيق ، تحليل عددي اندرکنش شمع - خاک روانگرا - سازه، با در نظر گرفتن ضخامت لايه روانگرا و تراز آب زيرزميني ، توسط نرم افزار فلک مورد بررسي قرار مي گيرد.
کلمات کليدي: شمع ، خاک روانگرا، FLAC، تحليل ديناميکي
١. مقدمه
اصطلاح روانگرايي در ابتدا توسط (١٩٥٣) Magami and Kudo مطرح شد که اين تعريف هم روانگرايي استاتيکي وهم روانگرايي ديناميکي را شامل مي شود. با توبه به کاربرد وسيع پي هاي شمعي ، ايمني شمع ها براي سازه ها در زمان زلزله از اهميت ويژهاي برخوردار است .
در زلزله هايي مانند آلاسکا (١٩٦٤)، نيگاتا (١٩٦٤)، لوماپريدا (١٩٨٩) هايوگوکن نامبو (١٩٩٥) و کوبه (١٩٩٥) ، حرکات جانبي غيريکنواخت خاک سبب افزايش ممان و برش در پي هاي شمعي شده است و در نتيجه گسيختگي در آنها به وقوع پيوسته است . تحقيق به عمل آمده پس از وقوع اين زلزله ها نشان مي دهد گسيختگي ها فقط در سرشمع ها بوجود نيامده است بلکه در قسمت هاي پايين تر نيز ترکها وگسيختگي مشاهده شده است [١]. اين پديده نشان مي دهد، که هم نيروي ناشي از سازه و هم اندرکنش سينماتيکي بين شمع و خاک، نقش مهمي در رفتار مکانيکي شمع دارد. در زمينه اندرکنش شمع - خاک روانگرا - سازه، آزمايش ها و تحليل هاي عددي زيادي در دهه اخير توسط افرادي همچون ; ١٩٩٢ ,Kagawa ; ٢٠٠٢ ,Finn and Fujita٢٠٠٥ Miwa at el صورت گرفته است .
اگر يک لايه خاک غير روانگرا روي يک خاک روانگرا حرکت کند، چنين جابه جايي براي فونداسيون شمعي بسيار مخرب است . در شکل (١) خرابي شمع ساختماني به علت جا به جايي دو متري در نيگاتا، نشان داده شده است . شکل (٢) شکستن کامل يک ستون در انباري در نزديکي شهر کوبه را نشان مي دهد[٢].
مدلهاي زيادي براي توليد فشار آب حفرهاي وجود دارند و از آنجايي که براي نمونه هاي خاصي در آزمايشگاه تهيه شده اند، براي شبيه سازي کامپيوتري کاربرد زيادي ندارند زيرا در برنامه هاي کامپيوتري مدل بايد جامع و کلي باشد. در اين تحقيق از مدل فين براي روانگرايي استفاده مي شود زيرا اولا ساده مي باشد وثانيا تناسب مناسبي با مسائل واقعي دارد.
شکل (١) خرابي پلي در زلزله ١٩٦٤ نيگاتا با تغيير مکان دو متري زمين [٢]
شکل (٢) برش شمع بوسيله تغيير مکان زمين در زلزله ١٩٩٥ کوبه [٢]
٢. مدل فين جهت توليد فشار آب حفرهاي [٣]
پاسخ اوليه ماسه به بارگذاري زلزله بستگي به مدول برشي اوليه ، Gm0 ، دارد. پاسخ ماسه تا زمان رسيدن به نقطه برگشت اول، از رابطه تنش -کرنش هايپربوليکي (١) که توسط زلاسکو و کندر بيان شده، تبعيت مي کند.
در رابطه (١) تنش برشي ، ، در کرنش ، ، با مدول برشي مماسي ماکزيمم اوليه ،Gm0 و تنش برشي ماکزيمم اوليه بيان مي شود. هاردين - درنويچ پارامتر Gm0 کيلونيوتن بر متر مربع ، براي لايه هاي افقي ماسه اي را با رابطه (٢) بيان نمودند:
رابطه (٢) با نسبت تخلخل e و تنش متوسط بيان مي شود.
اگر جهت بارگذاري در تغيير کند، آنگاه منحني تنش -کرنش در باربرداري و بارگذاري مجدد به صورت زير مي باشد:
در صورت عدم وجود فشار آب حفرهاي و سخت شوندگي ، روابط (١) و (٣) بيان کننده پاسخ تنش -کرنش ماسه مي باشد، و اين روابط وابستگي مدول برشي با کرنش و ميرايي هيسترتيک را نشان مي دهند. مارتين ، سيد و فين رابطه (٤) را جهت اعمال اثر سخت شوندگي بر رابطه تنش -کرنش ،ارائه داده اند:
در اين تنش برشي افقي ، کرنش برشي افقي ، تنش مؤثر متوسط و a و b پارامترهاي ثابتي هستند که با توجه به سيکل بارگذاري بدست مي آيند. ماکزيمم مدول برشي در سيکل nام ، از رابطه (٥) بدست مي ]يد:
بعد از وقوع کرنش حجمي . و با توجه به روابط (٤)، (٥) و روابط ارائه شده براي پارامترهاي a و b ، معادلات (٦) و (٧) نتيجه مي شود:
که در آن ، مدول برشي ماکزيمم ماسه خشک تنش برشي ماکزيمم ، ، کرنش حجمي و Hi ها مقادير ثابت مي باشند. در کرنش برشي ، رابطه ميان افزايش فشار آب حفرهاي، در آزمايش برش ساده زهکشي نشده و نمو کرنش حجمي ، ، در آزمايش برش ساده زهکشي شده، به صورت رابطه (٨) بيان مي شود:
که در آن Er، مدول برگشتي يک بعدي ماسه ، p n،تخلخل خاک، Kw، مدول بالک آب مي باشد. در مدل فين ، نمو کرنش حجمي با رابطه (٩) به کرنش حجمي تجمعي ، و کرنش برشي ، ، ارتباط مي يابد:
که در آن، Ciها وابسته به دانسيته نسبي و نوع ماسه هستند. بايرن، با ساده سازي رابطه (٩) را به صورت رابطه (١٠) بيان نمود و نشان داد که در بسياري موارد مي توان از رابطه (١١) و (١٢) استفاده نمود:[٤]
با استفاده از روابط (٨) تا (١٢) مي توان نمو فشار آب حفرهاي، را با کرنش ، در سيکل بارگذاري محاسبه نمود. مقدار جديد تنش مؤثر، بر مدول برشي ماکزيمم ، Gmn ، و تنش برشي ماکزيمم ، .، تأثيرگذار مي باشد. در نتيجه مدول و تنش برشي ماکزيمم مطابق با فشار آب حفرهاي و سخت شوندگي ،براي چرخه nام بارگذاري به صورت روابط (١٤) و (١٥) بيان مي شود:
در نتيجه معادله (٣) را مي توان به صورت رابطه (١٥) بيان نمود:
٣. عوامل مؤثر در تحليل ديناميکي [٥]
نکات مهم در تحليل ديناميکي عبارتند از: بارگذاري ديناميکي ، شرايط مرزي، ميرايي و انتقال موج در مدل . بارهاي ديناميکي را مي توان به صورت تاريخچه شتاب، سرعت ، تنش و نيرو اعمال نمود. در تحليل هاي ديناميکي مرزهاي ثابت و الاستيک سبب بازتاب امواج به داخل مدل مي شوند و با بزرگ گرفتن مدل اين بازتاب کاهش مي يابد زيرا ميرايي خود مصالح ، بيشتر انرژي موجهاي بازتاب شده را جذب مي کند ولي اين کار حجم محاسباتي بالايي را مي طلبد. براي جلوگيري از بزرگ کردن مدل، از ميدان آزاد در مرزها استفاده مي شود تا مرزها ويژگي جذب انرژي خود را حفظ کنند(شکل .(3
شکل (٣) مدل تحليل لرزهاي سطحي به همراه شبکه ميدان آزاد
در خاک و سنگ ميرايي طبيعي ، معمولا هيسترتيک مي باشد به اين علت در تحليل هاي ديناميکي از اين ميرايي جهت مدلسازي افت انرژي استفاده مي - شود و مقدار کمي ميرايي رايلي (٢%) براي حذف فرکانس بالا در نظر گرفته مي شود. در مدلسازي هاي عددي مش بندي نقش بسزايي در انتقال امواج دارد و اين نکته بايد مورد توجه قرار گيرد.
٤. مدلسازي
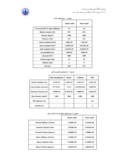
در اين تحقيق ، مطابق شکل (٤) لايه پاييني غير روانگرا ولايه بالايي داراي پتانسيل روانگرايي مي باشد. طول شمع برابر ١٥ متر و ارتفاع سازه ٥ متر مي - باشد. از مدل فين براي لايه روانگرا و مدل مورکولمب براي لايه غير روانگرا در حالت کرنش مسطح استفاده مي شود. تمامي عوامل مؤثر در تحليل ديناميکي در مدلسازي منظور شده است . پارامترهاي ورودي نرم افزار فلک مطابق جداول (١) تا (٣) مي باشد.