بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مقدمه
آتوماتاي سلولي در واقع يك مدل گسسته رياضي است كه در زمينه هاي مختلفي همچون تئوري محاسبات، رياضيات، فيزيك و ... كاربرد دارد.
آتوماتاي سلولي در اواخر دهه 1940 توسط John von Neumann مطرح و پس از او توسط رياضيداني بنام Ulam به عنوان مدلي براي بررسي رفتار سيستمهاي پيچيده پيشنهاد شد.
نامهاي ديگر آتوماتاي سلولي عبارتند از:
-cellular structures
-homogeneous structures
- tessellation structure
- iterative arrays
اسلاید 2 :
؟CA چرا
شبيه سازي سيستم هاي پيچيده نيازمند معادلات پيچيده مي باشد.
ارائه معادلات پيچيده نيازمند شناخت قوانين و وجود دانش کامل در مورد سيستم مورد بررسي است.
از معادلات پيچيده براي توصيف يک سيستم پيچيده استفاده نکنيد و بجاي آن اجازه دهيد اين پيچيدگي در قالب تعامل بين قوانين ساده بررسي گردد.
ايده : استفاده از تعاملات ساده بين سلولها در آتوماتاي سلولي براي شبيه سازي سيستمهاي پيچيده
اسلاید 3 :
مفاهيم اساسي در يك آتوماتاي سلولي
سلول
حالت
شبكه
تغيير و تحول (گسسته از لحاظ زماني)
همسايگي
قوانين تغيير حالت
وضعيت اوليه
اسلاید 4 :
سلول
اصلي ترين مولفه آتوماتاي سلولي
سلولها را مي توان بعنوان حافظه هايي كه وضعيت را ذخيره مي كنند در نظر گرفت.
معمولا حالت سلولها بطور همزمان بر اساس قوانين انتقال بروز رساني مي گردد.
اسلاید 5 :
حالت
حالات مي توانند وضعيت، عدد، رنگ و ... باشند.
تعداد حالاتي كه يك سلول مي تواند داشته باشد متناهي است.
اسلاید 6 :
شبكه
آتوماتاي سلولي شامل شبكه اي از سلولها است.
ابعاد شبكه يك مقدار متناهي است (يك بعدي، دو بعدي، سه بعدي و ...)
اسلاید 7 :
همسايگي
- همسايه هاي يك سلول در آتوماتاي سلولي بسته به كاربرد سلولهاي مختلفي از سلولهاي مجاور مي باشند.
اسلاید 8 :
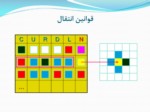
قوانين تغيير حالت
در آتوماتاي سلولي زمان گسسته است و در هر مرحله هر سلول، وضعيت جديد خود را با در نظر گرفتن حالت همسايههاي مجاور خود بر اساس يكسري از قوانين بدست ميآورد.
قانونها به سه دسته قابل تقسيم مي باشند:
1-قانون عمومي: در اين قانون مقدار يک سلول در مرحله بعدي، به مقدار تک تک سلولهاي همسايه در حالت فعلي وابسته است.
2- قانون totalistic: در اين قانون مقدار يک سلول در مرحله بعدي، به تعداد سلولهاي همسايه که در حالتهاي مختلف مي باشند، وابسته است. در اين نوع قانون برخلاف قانون عمومي، توجه اي به تک تک سلولها نمي شود.
3- قانون outer totalistic: تنها تفاوتي که اين قانون با totalistic دارد در اين است که در تعيين حالت بعدي سلول، حالت فعلي نيز موثر است.
اسلاید 9 :
مثال: آتوماتاي سلولي ابتدائي (يك بعدي)
در اين آتوماتا هر سلول داراي دو حالت صفر يا يك مي باشد.
همسايه هاي هر سلول دو سلول كناري آن مي باشند.
هر سلول بهمراه دو همسايه كناري آن مي توانند هشت مقدار مختلف داشته باشند.
هر سلول با توجه به وضعيت فعلي خود و دو همسايه اش يكي از حالات زير را خواهد داشت:
اسلاید 10 :
مثال: آتوماتاي سلولي ابتدائي (يك بعدي)
هر سلول در مرحله بعد مي تواند داراي يكي از دو حالت صفر يا يك باشد.
به ازاي هشت نوع همسايگي مختلف ما 256 نوع آتوماتاي سلولي يك بعدي مي توانيم داشته باشيم.
هر كدام از اين آتوماتاها داراي قانون خاص خود مي باشند.
شماره گذاري قانونها بسته به وضعيتي كه در حالات مختلف سلول خواهد داشت انجام مي شود. براي مثال قانون زير به قانون 30 معروف است.