بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مقدمه
ايده اصلي روش
طراحي يک کنترلکننده قطري براي يک تابع تبديل مربعي پس از دکوپله کردن نسبي
تفاوت و تشابه با روش .C.L
هردو مبتني بر تئوري نايکوييست تعميم يافته
استفاده مستقيم از تابع تبديل در روش آرايه نايکوييست
محدوديتها
لزوم مربعي بودن تابع تبديل
لزوم تبديل تابع تبديل به فرم غالب قطري
اسلاید 2 :
ساختار کنترلکننده
يک ساختار مناسب:
جبرانساز معکوسپذير و گويا با صفرها و قطبهاي سمت چپ
قضيه Rosenbrock (1970):
طراحي دو مرحلهاي:
غالب قطري کردن ماتريس حلقهباز
طراحي کنترلکنندههاي SISO براي هر حلقه بدون نگراني نسبت به اندرکنش باقيمانده در سيستم
اسلاید 3 :
يادآوري
ايده اصلي : نايکوييست تعميم يافته
نبايد داخل باند گرشگورين
قرار گيرد.
DD باشد
در عمل:
در محدوده فرکانسي گستردهاي تا حد زيادي DD ميشود
نشد DD
با يک جبرانساز قطري باند گرشگورين را
از 1- دور ميکنيم بدون اينکه پهناي آن
را زياد تغيير دهد.
اسلاید 4 :
مقايسه INA و DNA
INA
ِRDD کردن ماتريس
تشخيص دقيقتر رفتار سيستم حلقهبسته
از اطلاعات سيستم حلقه باز
DNA
CDD کردن ماتريس
آزادي عمل بيشتر در انتخاب
کنترلکننده
اسلاید 5 :
دستيابي به فرم غالب قطري
مهمترين مساله در روشهاي آرايه نايکوييست
نکته: براي بعضي فرايندها اساسا دستيابي به فرم غالب قطري ممکن نيست
چند روش دستيابي به فرم غالب قطري:
1- سعي و خطا(ي هوشمند)
2- پرون – فروبنيوس
3- شبه قطريسازي
اسلاید 6 :
دستيابي به فرم غالب قطري
سعي و خطاي هوشمندانه
جابجايي وروديها با ماتريسهاي تبديل
استفاده از ماتريسهاي تبديل مقدماتي
دکوپله کردن در يک فرکانس خاص
نکات:
استقلال DD بودن يک ماتريس و معکوس آن
مجوز ضرب هرستون جبرانساز CDD کننده در يک تابع اسکالر
مجوز ضرب هرسطر جبرانساز RDD کننده در يک تابع اسکالر
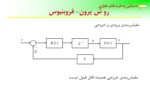
اسلاید 7 :
رو ش پرون- فروبنيوس
مقياسبندي ورودي و خروجي
مقياسبندي خروجي هميشه قابل قبول نيست
اسلاید 8 :
دستيابي به فرم غالب قطري
روش پرون- فروبنيوس
هر ماتريس مربعي اوليه مثبت مانند M داراي مقدار ويژه حقيقي و مثبت
بزرگتر است و همه عناصر بردار ويژه آن به صورت حقيقي و مثبت قابل تعيين است.
با عناصر مثبت و حقيقي
x بردار ويژه راست پرون- فروبنيوس ماتريس M
تبديل رابطه به تساوي
کاربرد در محاسبه پيشجبرانساز قطري براي RDDکردن :
اگر پيشجبرانساز قطري
به طوري که
اسلاید 9 :
نتيجه:
کمترين مقدار عبارت فوق ،
ميباشد،که معادل بيشترين درجه DD شدن است
و به ازاي انتخاب عناصر قطر
مساوي عناصر بردار ويژه راست پرون- فروبنيوس
ماتريس
بدست ميآيد
نکته: اگر در فرکانسي
دستيابي به ماتريس DD در آن فرکانس با اين روش ممکن نيست
مساله: تحقق جبرانساز
روشهاي پيشنهادي:
1- استفاده از ماتريس ثابت T به جاي M
2- طراحي جبرانساز ديناميکي
به طوري که تغييرات مشخصه فرکانسي
دامنه عناصر آن مشابه تغييرات مشخصه فرکانسي دامنه عناصر بردار ويژه راست
پرون- فروبنيوس
باشد
اسلاید 10 :
مثال:
معکوس ماتريس
رسم دواير گرشگورين