بخشی از مقاله
این مقاله به دلیل نمودار و جداول زیاد امکان قرار دادن روی سلیت را ندارد.
در صورت هرگونه سوال تماس حاصل نمایید.
جامعه و نمونه
مقدمه
هدف اين پروژه، بررسي ارتباط بين استفاده دانش آموزان از كامپيوتر و عملكرد آنها در مدرسه مي باشد. براي يك دانش آموز كاملاً عادي است كه بشنود: « چرا اينقدر وقت خود را با كامپيوتر تلف مي كني؟» « چرا به تكاليفت كمتر از كامپيوتر اهميت مي دهي؟» و ...
بيشتر دانش آموزان دوست ندارند نصيحت هاي خانواده هايشان را گوش كنند ولي آيا اين دانش آموزان به اندازه ي كافي درس مي خوانند؟ آيا براي استفاده از كامپيوتر برنامه اي دارند؟ آيا از كامپيوتر استفاده ي درست مي كنند؟ چقدر وقت خود را با استفاده كامپيوتر مي گذرانند؟ 2 ساعت يا 3 ساعت در روز؟ ...
بعضي ها، خصوصاً خانواده ها، معتقدند كه كامپيوتر به درس و تحصيل دانش آموزان ضرر مي زند. آيا واقعاً اين چنين است؟
اين پروژه با توزيع پرسشنامه بين دانش آموزان آغاز گشت. در اين رابطه داده ها جمع آوري شده و مورد ارزيابي و تجزيه و تحليل قرار گرفتند. در اين بررسي از محاسبات آماري، نمودارها و ... استفاده شد.
جامعه و نمونه
جمع آوري داده ها
دانش آموزان سال دوم دبيرستان به عنوان جامعه آماري در نظر گرفته شدند و 15 دانش آموز به طور تصادفي از بين دانش آموزان سال دوم دبيرستان اين مدرسه به عنوان نمونه انتخاب شدند.
جمع آوري داده ها به روش تهيه پرسش نامه انجام شد. در اين نظر خواهي، اسامي خواسته نشده بود تا دانش آموزان بتوانند با راحتي خيال پاسخ هاي خود را بدهند. اگر جمع آوري اطلاعات به وسيله مصاحبه انجام مي شد، ممكن بود دانش آموزان پاسخ هاي درست ندهند و نيز زمان بيشتري مورد نياز بود.
در پرسش نامه تهيه شده، از طول مدت زمان و چگونگي استفاده دانش آموزان از كامپيوتر سؤال شد و اين كه چند ساعت در روز درس مي خوانند و سؤال هايي از اين قبيل. يك نسخه از اين پرسش نامه، ضميمه ي اين تحقيق شده است.
بخش دوم
جداول داده ها
اين فصل شامل جداول مورد نياز براي ترسيم نمودار است. كه در آنها معيار هايي نظير: فراواني، فراواني نسبي، درصد فراواني، فراواني تجمعي، مركز دسته و ... مشخص شده است.
اطلاعات استخراج شده از پرسشنامه ها نيز در جداولي در انتهاي همين بخش آمده است كه با كمك آنها نمودار هاي مقايسه اي رسم مي شود.
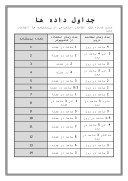
جداول داده ها
جدول شماره يك: جدول فراواني معدل دانش آموزان
فراواني تجمعي درصد فراواني فراواني نسبي مركز دسته فراواني دسته ها
4 29 29/0 125/19 4 19 تا 25/19
5 7 07/0 375/19 1 25/19 تا 5/19
8 21 21/0 625/19 3 5/19 تا 75/19
14 43 43/0 875/19 6 75/19 تا 20
- 100 1 - 14 جمع
جدول شماره دو: جدول موارد استفاده از كامپيوتر
در صد فراواني فراواني موضوع
40 8 بازي و سرگرمي
25 5 برنامه نويسي و گرافيك
10 2 برنامه هاي آموزشي
25 5 اينترنت
100 20 جمع
جداول داده ها
جدول شماره سه: جدول فراواني زمان استفاده از كامپيوتر
درصد فراواني فراواني زمان
0 0 صبح
21 3 ظهر
36 5 بعد از ظهر
14 2 شب
29 4 نا معلوم
100 14 جمع
جدول شماره چهار: جدول فراواني زمان مطالعه دروس مدرسه
درصد فراواني فراواني زمان
11 2 صبح
0 0 ظهر
66 12 بعد از ظهر
17 3 شب
6 1 نا معلوم
100 18 جمع
جداول داده ها
جدول شماره پنج: اطلاعات استخراجي از پرسشنامه ها (با انجام محاسبات)
مدت زمان مطالعه دروس مدت زمان استفاده از كامپيوتر شماره پرسشنامه
28 1 1
5/24 2 2
21 2 3
5/17 4 4
14 3 5
14 5/0 6
14 1 7
21 5/2 8
21 3 9
5/10 3 10
5/31 7 11
21 8 12
21 6 13
21 3 14
* تمامي داده ها بر حسب ساعت در هفته است.
جداول داده ها
جدول شماره شش: اطلاعات استخراجي از پرسشنامه ها (اطلاعات خام)
مدت زمان مطالعه دروس مدت زمان استفاده از كامپيوتر شماره پرسشنامه
4 ساعت در روز 1 ساعت در هفته 1
3 الي 4 ساعت در روز 2 ساعت در هفته 2
3 ساعت در روز 2 در هفته 3
2 الي 3 ساعت در روز 4 در هفته 4
2 ساعت در روز 3 ساعت در هفته 5
2 ساعت در روز 5/0 ساعت در هفته 6
2 ساعت در روز 1 ساعت در هفته 7
حدود 3 ساعت در روز 2 الي 3 ساعت در هفته 8
3 ساعت در روز 3 ساعت در هفته 9
5/1 ساعت در روز 3 ساعت در هفته 10
4 الي 5 ساعت در روز 7 ساعت در هفته 11
حداكثر 3 ساعت در روز 8 ساعت در هفته 12
3 ساعت در روز 6 ساعت در هفته 13
3 ساعت در روز 3 ساعت در هفته 14
جداول داده ها
جدول شماره هفت: جدول معدل سال گذشته دانش آموزان
معدل شماره پرسشنامه
87/19 1
50/19 2
11/19 3
94/19 4
89/19 5
12/19 6
07/19 7
82/19 8
54/19 9
25/19 10
51/19 11
80/19 12
75/19 13
91/19 14
بخش سوم
محاسبات آماري
الف) معدل
نمرات به دست آمده از پرسشنامه ها به شرح زير است: (به ترتيب صعودي)
19.07 | 19.11 | 19.12 | 19.25 | 19.50 | 19.51 | 19.54 | 19.75 | 19.80 | 19.82 | 19.87 | 19.89 | 19.91 | 19.94
________________________________________
دامنه تغيرات:
اگر
a = كوچكترين داده
b = بزرگترين داده
بنابراين
R = b - a (R = دامنه تغييرات)
حال عمل جايگزيني را انجام مي دهيم:
R = 19.94 - 19.07 = 0.87 ~ 1
حالا طول دسته را از رابطه زير به دست مي آوريم با فرض اينکه تعداد دسته ها 5 باشد:
طول دسته = دامنه تغيرات / تعداد دسته ها
طول دسته = 25/0
محاسبات آماري
ميانه:
M = (19.54 + 19.75) / 2 = 19.65
________________________________________
ميانگين:
براي محاسبه ميانگين از فرمول ميانگين زير استفاده مي کنيم:
ax + b = ax + b
بنابراين هر داده را به شکل زير مي نويسيم:
19 + 07 * 0.01
19 + 11 * 0.01
19 + 12 * 0.01
19 + 25 * 0.01
...
سپس ميانگين اين اعداد را حساب مي کنيم:
(7 + 11 + 12 + 25 + 50 + 51 + 54 + 75 + 80 + 82 + 87 + 89 + 91 + 94) / 14 ~ 58
19 + 58 * 0.01 = 19.58
نمودار جعبه اي شماره 1 )
واريانس و انحراف از معيار:
واريانس برابر ميانگين مجذور انحرافات از ميانگين است. بنابراين:
[(19.07-19.58)2 + (19.11-19.58)2 + (19.12-19.58)2 + …] / 14= 0.1 2 = 0.1 = 0.32
محاسبات آماري
ب) ساعات مطالعه دروس
ساعات مطالعه دروس به دست آمده از پرسشنامه ها به شرح زير است: (به ترتيب صعودي)
10.5 | 14 | 14 | 14 | 17.5 | 21 | 21 | 21 | 21 | 21 | 21 | 24.5 | 28 | 31.5
براي واقعي تر شدن نتيجه، كوچكترين و بزرگترين استثناي اين داده ها را خط زديم.
________________________________________
دامنه تغييرات:
اگر
a = كوچكترين داده
b = بزرگترين داده
بنابراين
R = b - a (R = دامنه تغييرات)
حال عمل جايگزيني را انجام مي دهيم:
R = 28 - 14 = 14
________________________________________
ميانه:
M = (21 + 21) / 2 = 21
________________________________________
ميانگين:
براي محاسبه ميانگين به صورت زير عمل مي كنيم:
[(3*14) + (1*17.5) + (6*21) + (1*24.5) + (1*28)] / 12 = 19.84
نمودار جعبه اي شماره 2 )
محاسبات آماري
واريانس و انحراف از معيار:
[(14-19.84)2 + (14-19.84)2 + … + (28-19.84)2] / 12= 17.01 2 = 17.01 = 4.12
*****
ج) ساعات استفاده از كامپيوتر
ساعات به دست آمده از پرسشنامه ها به شرح زير است: (به ترتيب صعودي)
0.5 | 1 | 1 | 2 | 2 | 2.5 | 3 | 3 | 3 | 3 | 4 | 6 | 7 | 8
________________________________________
دامنه تغييرات:
اگر
a = كوچكترين داده
b = بزرگترين داده
بنابراين
R = b - a (R = دامنه تغييرات)
حال عمل جايگزيني را انجام مي دهيم:
R = 8 – 0.5 = 7.5
________________________________________
ميانه:
M = (3 + 3) / 2 = 3
________________________________________
ميانگين:
براي محاسبه ميانگين به صورت زير عمل مي كنيم:
[(1*0.5) + (2*1) + (2*2) + (1*2.5) + (4*3) + (4) + (6) + (7) + (8)] / 14 = 3.29
نمودار جعبه اي شماره 3 )
واريانس و انحراف از معيار:
[(0.5-3.29)2 + (1-3.29)2 + … + (8-3.29)2] / 14= 4.74 2 = 4.74 = 2.18
*****