دانلود مقاله تحقیق درس امار

بخشی از مقاله

تحقیق درس امار

در يك پاركينگ 950 ماشين پارك شده است. شخصي مي خواهد با استفاده از اعداد تصادفي نمونه خود را انتخاب كند. (يك نمونه ي 30 تايي از ماشين هاي پارك شده)

پس از اينكه او نمونه ي خود را انتخاب كرد متوجه شد كه 8 ماشين پيكان، 7 ماشين ريو، 5 ماشين پژو، 3 ماشين فولكس، 3 ماشين پاترول، 3 ماشين دوو و يك ماشين بنز بود. هدف شخص به دست آوردن نام ماشين و سال ماشين هاي مي‌باشد.

جامعه و نمونه
جامعه- كليه اي ماشين هاي پارك شده در داخل پاركينگ و موضوه مورد مطالعه يك نمونه تصادفي 30تايي از ماشين هاي پارك شده.
نمونه- حد 30 اتومبيل از ميان 950 اتومبيل براي بررسي كه بيانگر خصوصيات جامعه است.
نمونه تصادفي ساده- اگر كليه ي ماشين ها را به عنوان جامعه آماري در نظر بگيريم. كه نمونه انتخاب شده كاملاً تصادفي است و قبل از انتخاب همه ي افراد جامعه به طور يكسان امكان و سهم برگزده شدن را داشته اند.

روش جمع آوري داده ها
روش جمع آوري داده در اين مرحله مشاهده و ثبت وقايع است بدين ترتيب كه پس از انتخاب آنان فرد اطلاعات لازم را از ماشين يادداشت برداري مي‌كند.
متغير تصادفي
اگر اندازه گيري بر اساس سال ماشين ها باشد متغير تصادفي آن كمي پيوسته مي‌باشد.
دسته بندي داده ها و جدول فراواني
داده ها 1345-1330-1375-1341-1350 پيكان
1360-1376-1355
1369-1372-1383-1381-1366-1352-1344 ريو

1333-1382-1377-1373-1359 پژو
1346-1335-1330 فولكس
1367-1374-1380 پاترول
1364-1373-1384 دوو
1350 بنز
داده ها به صورت مرتب شده

كوچكترين داده- بزرگترين دادة دامنه تغييرات
54=1330-1384= دامنة تغييرات
ـــــــــــــــــــ = حدود دسته

حدود دسته
1330 1330 1333 1335 1341
1344 1345 1346 1350 1350

1352 1355 1359 1360 1364
1366 1367 1369 1372 1373
1373 1374 1375 1374 1377
1380 1381 1382 1383 1384
حدود دسته
ـــــــــــــــــــــــ = فراواني نسبي
فراواني دسته هاي ماقبل+ فراواني هر دسته= فراواني تجمعي
ـــــــــــــــــــــــــــــــ = مركز دسته

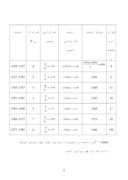
دسته فراواني fi فراواني نسبي درصد فراواني نسبي مركز دسته فراواني تجمعي
1337-1329 4


4
1345-1337 2

1341 6
1353-1345 5

1349 11
1361-1353 3

1357 14
1369-1361 3

1365 17
1377-1369 7

1373 24
1385-1377 6

1381 30*
نكته: اگر دامنه ي تغييرات برابر صفر شود يعني تمام داده ها با هم برابر است.
نمودارها و تحليل داده ها
شاخص هاي هندسي: براي تحليل داده ها مي توانيم از اشكال هندسي استفاده كنيم كه اين اشكال عبارتند از:
1-نمودار ميله اي 2-نمودار مستطيلي 3-نمودار دايره اي
4-چند بر فراواني 5-ساقه و برگ 6-جعبه اي
نمودار ميله اي: براي رسم نمودار ميله اي از فراواني ها استفاده مي كنيم و نام آن را زير آن مي
نويسيم و اگر از مقياس خاصي استفاده كرد. باشيم آن مقياس را كنار نمودار مي نويسيم.

نمودار ميله اي

نمودار مستطيلي: اين نمودار براي داده هاي پيوسته مناسب است و بر اساس فراواني ها رسم مي شود و نام آن در زير نمودار نوشته مي شود.

نمودار مستطيلي

نمودار دايره اي
براي رسم نمودار دايره اي قطاع را به دست مي آوريم.
360*فراواني نسبي= قطاع
قطاع
8/46=360*13/0
6/21=360*06/0
6/57=360*16/0
36=360*1/0
36=360*1/0
8/82=360*23/0
72=360*2/0
نمودار دايره اي
چند برابر فراواني، از مراكز دسته ها استفاده كرده و مراكز دسته ها را به امتداد فراواني به هم وصل مي كنيم. در اين حالت براي زيبايي نمودار يك دسته فرضي قبل و بعد از آن ايجاد مي كنيم و با پيدا كردن مراكز آن دسته ها به نمودار متصل مي كنيم.

نمودار چندبر فراواني
ساقه و برگ
اين نمودار براي داده هايي است كه به صورت اعداد طبيعي باشند ابتدا داده ها را مرتب و بر اساس عدد دهگان و صدگان دسته بندي مي كنيم.
ساقه برگ به دليل اين كه سال 1300 در همه مشترك بود در نمودار ساقه و برگ ذكر نشد.
3 5 3 0 0
4 6 5 4 1
5 9 5 2 0 0
6 9 7 6 4 0
7 7 6 5 4 3 3 2
8 4 3 2 1 0
شاخص هاي مركزي
مد: داده اي است كه بيشترين فراواني را دارد.
ميانه: پس از مرتب كردن داده ها، مقداري را كه تعداد داده هاي بعد از آن با تعداد داده هاي قبل از آن برابر است، ميانه مي ناميم.
1330 1330 1333 1335 1341 1344 1345
1346 1350 1350 1352 1355 1359 1360
1364 1366 1367 1369 1372 1373 1373
1374 1384 1376 1377 1380 1381 1382
1383 1384
روش محاسبه ميانه:
اگر تعداد داده ها زوج باشد آن را تقسيم بر دو مي كنيم و بعد از آن به اضافه ي 2 تقسيم بر 2 مي كنيم و دو عدد به دست آمده را با هم جمع و تقسيم بر دو مي كنيم.
1373 و 1350 و 1330= مد
شماره ميانه 15=

شماره ميانه
نمودار جعبه اي براي نشان دادن متقارن بودن داده ها است.
ابتدا كوچكترين داده و بزرگترين داده را مشخص مي كنيم، سپس ميانه ي داده ها را مشخص مي كنيم. ميانه نيمه اول داده ها را كه به آن چارك اول و ميانه ي نيمه ي دوم داده ها كه به آن چارك سوم مي گوييم را به دست مي آوريم.
شماره شماره 1330= ك.د
1384=ب.د

ميانگين، براي به دست ميانگين اعداد و و… به صورت زير عمل مي كنيم.

ميانگين وزن دار:براي محاسبه ميانگين در جدول فراواني اگر جدول شامل حدود دسته باشد ابتدا نشان دسته را محاسبه مي كنيم. سپس نشان هر دسته را در فراواني آن دسته ضرب مي كنيم و در ستون جديد مي نويسيم. مجموع اعداد اين ستون را تقسيم بر مجموع فراواني ها مي كنيم.