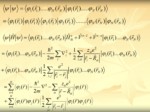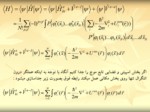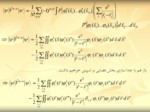بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
تقریب Born-Upenhimer
هامیلتونی یک سیستم الکترونی عبارت است از:
اسلاید 2 :
اصل اين تقريب بر اين فرض استوار است كه چون جرم يونها از الكترونها بسيار بيشتر است، لذا ميتوان از حركت يونها در برابر الكترونها صرف نظر كرد. بنا براين ميتوان نوشت:
اسلاید 3 :
كه درآن تابع توصيف كننده حركت يونها و تابع توصيف كننده حركت الكترونها ميباشد و منظور از مكانهاي تعادل ذرات شبكه است كه يونها در اين مكانها ثابت فرض ميشوند. نتيجه نهايي اين تقريب رسيدن به دو معادله مجزا است :
اسلاید 4 :
تقریب Born-Upenhimer
هامیلتونی یک سیستم الکترونی عبارت است از:
اسلاید 5 :
اصل اين تقريب بر اين فرض استوار است كه چون جرم يونها از الكترونها بسيار بيشتر است، لذا ميتوان از حركت يونها در برابر الكترونها صرف نظر كرد. بنا براين ميتوان نوشت:
اسلاید 6 :
باز هم با جدا سازی بخش فضایی و اسپینی خواهیم داشت :
اسلاید 7 :
حال از نتیجه بدست آمده با توجه به قید سیستم وردش می گیریم.
با جایگذاری نهایتا ً به دسته معادلات HF میرسیم:
منظور از موازی بودن اسپین الکترون iام وjام است.
اسلاید 8 :
نکاتی در مورد تقریب Hartree-Fock :
1) دسته معادلات بدست آمده غیر خطی هستند و باید به روش خود سازگار حل شوند.
2) پتانسیل موجود در معادلات یک عملگر غیر موضعی است.
3) انتخاب تابع موج سیستم بس الکترونی بصورت دترمینان هنوز هم نوعی انتخاب خاص است وموجب محدودیت فضایی میشود. لذا اصل وردش ما را مطمئناً به مینیموم انرژی نمی رساند.
به طور کلی می توان گفت:
اسلاید 9 :
قضیه Koopman
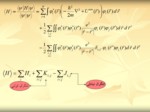
سیستمی N الکترونی در نظر بگیرید که ویژه مقادیردسته معادلات HF آن باشند. بنابراین قضیه با جدا کردن الکترونk ام از سیستم تغییری در انرژی تبادلی و انرژی کولنی و ویژه مقادیر دیگر الکترونها در سیستم N-1) ) ذره ای ایجاد نمیشود.
لذا به معنای دقیقتر قضیه Koopman بیان میکند که انرزی برانگیختگی سیستم عبارت است از ویژه مقدار الکترون در تقریب HF
اسلاید 10 :
جمله تبادلی درنظریه HF
جهت درک بهتری از جمله تبادلی در نظریهHF میخواهیم احتمال یافتن الکترون اول در بازه تا والکترون دوم در بازه تا را در یک سیستمN الکترونی محاسبه کنیم.
باز هم از شکل فشرده دترمینان Slater استفاده میکنیم :
با جایگذاری خواهیم داشت :