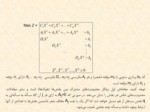بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
به طور كلي مسائل برنامهريزي خطي به دو گروه عمده قابل تقسيم هستند: مسائل داراي ساختاري خاص و مسائل فاقد اين ويژگي. شايد با بعضي از مسائل مانند مدل حمل و نقل، تخصيص و يا شبكهها كه ساختاري خاص دارند، آشنا باشيد. اين مسائل به علت داشتن اين ويژگي امكان استفاده از الگوريتمهاي كارا تري از سيمپلكس را يافته و اين امر موجب كاهش محاسبات ميگردند.
دانتزيگ (Dantzig) تكنيكهاي محاسباتي كارا را به منظور كاهش محاسبات به دو گروه تقسيم ميكند. تكنيكهايي كه موجب «كاهش تعداد تكرارها» ميگردد و تكنيكهايي كه «موجب فشرده شدن ماتريس معكوس» ميشود. «الگوريتم اوليه - ثانويه» و «الگوريتم تجزيه» به ترتيب نمونههايي از اين دو گروه هستند.
اسلاید 2 :
انواع خاص مسائل برنامهريزي خطي كه در اين قسمت معرفي ميگردد، «مسائل بزرگ مقياس (large-scale)» است كه تعداد بسيار زيادي محدوديت و متغير دارند. از خصوصيات مهم اينگونه مسائل با ابعاد بزرگ آن است كه بسياري از ضرايب متغيرهاي تصميم در محدوديتهاي مسأله، صفر هستند، و در بعضي از انواع مشخص، صرفاً معدودي ضرايب غير صفر وجود دارد. در نتيجه، به منظور ايجاد شكل ساده و كاراتري از روش سيمپلكس ميتوان از ساختار رياضي خاص آنها استفاده كرد و ميزان محاسبات لازم را تا حد زيادي كاهش داد. در شكل صفحهي بعد چهار نوع از مسائل بزرگ مقياس را مشاهده ميكنيد. در اين شكل فقط ساختار ضرايب غير صفر نشان داده شده است.
اسلاید 3 :
اين نوع مسائل وضعيت شركتهاي بزرگي را نشان ميدهد كه شركتهاي كاملاً مستقلي را تحت پوشش داشته و هيچ نظام كنترل متمركزي براي اداره و يا كنترل آنها به كار نميگيرد. مدل اين نوع مسائل به صورت زير است.
اسلاید 4 :
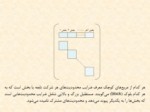
يكي از متداولترين مسائل برنامهريزي خطي بزرگ مقياس، مسائل چند بخشي است. مسائل چندبخشي بيانگر وضعيت شركتهاي بزرگي است كه تعدادي شركتهاي فرعي تحت پوشش با بخشهاي مختلف و نسبتاً مستقل از هم دارند. از آنجا كه هريك از بخشهاي شركت صرفاٌ به دنبال بهينه كردن عمليات مربوط به خود است لذا مسأله تقريباٌ به چند مسأله فرعي تجزيه ميشود. اما شركت مادر به منظور ايجاد هماهنگي، كنترل و اعمال سياستهاي كلي خود بر شركتها يا بخشهاي تابعه، منابع و امكانات مشتركي را بين آنها تقسيم ميكند كه اين منابع و امكانات در قالب مجموعه محدوديتهايي كه در شكل صفحه بعد به صورت مستطيل ظاهر ميشود، ارائه ميگردند.
اسلاید 5 :
هر كدام از مربعهاي كوچك معرف ضرايب محدوديتهاي هر شركت تابعه يا بخش است كه به هر كدام بلوك (block) ميگويند. مستطيل بزرگ و بالايي شامل ضرايب محدوديتهايي است كه بخشها را به يكديگر پيوند ميدهد و محدوديتهاي مشترك ناميده ميشود.
اسلاید 6 :
شبيه مسائل چند بخشي، مسائل چند دورهاي تقريباً قابل تجزيه به چند قسمت است. هر بخش در اين وضعيت، به دنبال بهينه كردن عمليات سازماني خود در دورهي زماني برنامهريزي است. در اين نوع مسائل براي هماهنگي فعاليتها در دورههاي زماني مختلف به منظور بهينه كردن عمليات براي تمامي افق برنامهريزي، وجود محدوديتهاي مشترك ضرورت پيدا ميكند. صورتبندي اين نوع مسائل كه در آن برنامهريزي جامع چندين دورهي زماني مد نظر است به مسائل چند دورهاي (دوره به معني روز، ماه، سال و غيره) ميانجامد.
اسلاید 7 :
در جهان واقع مسائل بسياري وجود دارد كه همزمان خصلت چندبخشي و چنددورهاي دارد. اين نوع از مسائل معمولاً داراي تعداد زيادي مسائل فرعي است كه هدف هر مسأله بهينه كردن عمليات براي هر بخش و در هر دوره است. اين نوع مسائل داراي تعدادي متغيرهاي رابط و محدوديتهاي مشترك هستند.
اسلاید 8 :
الگوريتم تجزيه يا به عبارت دقيقتر، الگوريتم تجزيهي دانتزيك – ولف (Dantzig-Wolf decomposition algorithm) غالباٌ توانايي حل مسائل بسيار بزرگ را داد. هرگاه ماتريس ضرايب مسألهاي داراي ساختاري خاص به صورت مسائل چند بخشي باشد، كارايي اين الگوريتم بسيار توسعه مييابد. همانطور كه قبلاٌ گفته شد اين نوع مسائل داراي بخشها (بلوكها) ي مستقلي هستند كه با تعدادي محدوديت به هم پيوند داده ميشوند.
الگوريتم تجزيه بر اساس اين چهار مفهوم بنيان شدهاست:
1- الگوريتم سيمپلكس تجديد نظر شده
2- نمايش مجموعهي محدب بر حسب نقاط گوشهاي
3- روش كاهش محدوديتها
4- روش توليد ستون
اسلاید 9 :
منطقهي موجه مسائل برنامهريزي خطي، نمونهاي از مجموعهاي محدب است. مجموعه محدبي را در صفحه در نظر بگيريد. نقاطي كه گوشههاي مجموعه را تشكيل ميدهند، نقاط گوشهاي (extreme points) ناميده ميشود، يعني نقطهاي از مجموعهي محدب را كه بر روي پارهخطي كه دو نقطهي ديگر از مجموعه را به هم وصل ميكند قرار ندارد نقطهي گوشهاي مينامند.
مفهوم ديگري كه در اين بخش با آن آشنا ميشويد، مفهوم تركيب محدب (convex combination) است.
بردار (نقطهي) X در فضاي En تركيبي خطي (linear combination) از بردارهاي (نقاط) X1, X2, …, Xn است. اگر X برابر باشد با يعني در رابطه فوق مقادير ثابت هستند كه ميتوانند هر عدد حقيقي مثبت يا منفي باشند.
اسلاید 10 :
هر تركيب خطي در فضاي دو بعدي، يك خط و در فضاي سه بعدي يك صفحه تعريف ميكند. هرگاه در تركيبي خطي مقادير ، مقاديري غير منفي بوده و مجموع آنها برابر با يك باشد ،تركيب محدب تعريف ميشود. يعني بردار X تركيبي محدب از بردارهاي X1، X2 و ... Xn است اگر
مجموعهي تمام تركيبات محدب بردارهاي X1, X2 در فضاي دو بعدي پارهخطي مستقيم است كه شامل نقاط پاياني اين دو بردار نيز هست.
مجموعهي تمام تركيبات محدب نقاط، پوستهي محدب (convex hull) را تشكيل ميدهد. پوسته محدب هر دو نقطهاي از En پارهخطي است كه آن نقاط را به هم وصل ميكند، و پوستهي محدب هر سه نقطهي متمايز در صفحه (كه همهي آنها روي يك خط نباشند) يك مثلث است و پوستهي محدب مجموعهي تمام نقاطي كه بر محيط دايرهاي واقعند دايرهي توپري است كه محيط دايره مرز آن است.
نقطهاي را در مجموعهاي محدب، نقطهي گوشهاي مينامند اگر آن نقطه را نتوان بر حسب تركيب محدب هيچ دو نقطهي ديگر از آن مجموعهي محدب نوشت.