دانلود فایل پاورپوینت نمونه سوالات کنکور رشته علوم کامپیوتر

بخشی از پاورپوینت

--- پاورپوینت شامل تصاویر میباشد ----

اسلاید 1 :

سوال اول

پیچیدگی زمانی الگوریتم زیر از چه درجه ای است ؟

int F(int n , int m)

if (n < = 1 || m < = 1 )retarn 1 ;

return  n  + m * F (n-1) , m / 2 ) ;

1)n                                              2) log m                       

3) min ( n , log m )                4) max ( n , log m )

اسلاید 2 :

پاسخ سوال اول

گزینه (3) صحیح است .

n   بار یک واحدکم می شود پس بر حسب زمان n زمان خطی است و چون m هربار نصف می شود ، بر حسب m لگاریتمی است و هر کدام زودتر به 1 یا کوچکتر از 1 برسند الگوریتم خاتم می یابد .

اسلاید 3 :

سوال دوم

—برای پیدا کردن  عدد میانه(median )   بین n عدد در حالتی که    3 = n  و 5 = n  باشد به ترتیب حداقل  چند مقایسه نیاز داریم ؟ ( از چپ به راست )

1) 6 و 3                                  2) 10 و 3

3) 6 و 2                                  4) 10 و 2

اسلاید 4 :

پاسخ سوال دوم

گزینه (1) صحیح است .

اسلاید 5 :

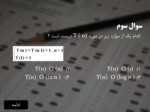
سوال سوم

کدام یک از موارد زیر در مورد T ( n) درست است ؟

1) T(n)  O (1)                           2)  T(n)  O (n)

3) T(n)  O (log n )                   4) T(n)  O (ln n ) 

اسلاید 6 :

پاسخ سوال سوم

گزینه (4) صحیح است .

Lnn =1+...+ 1+ 1 + = T(n)

اسلاید 7 :

سوال چهارم

الگوریتمی که زمان آن به وسیله فرمول بازگشتی زیر بیان شود دارای چه پیچیدگی می باشد ؟ (  i یک عدد ثابت دلخواه n > i  < 1 )

1)  O (n )                         2)    ( n 2 ) O

 3 ) O ( n log n )              4) ( 2n ) O

اسلاید 8 :

پاسخ سوال چهارم

گزینه (4) صحیح است .

مثلاً اگر 2 = i   آنگاه (2 n)o = ( 2- n ) T + n = T(n)

اسلاید 9 :

سوال پنجم

فرض کنید    a = log n!  ,b = n log n , c = log n , d = n  یک الگوریتم مرتب سازی بر مبنای درخت تصمیم گیری حداقل دارای چه تعداد مقایسه خواهد بود ؟

1) a   

2 ) a , b            

3) a , c           

4 ) b , d

اسلاید 10 :

پاسخ سوال پنجم

گزینه (2) صحیح است .

حداقل تعداد مقایسه در روش های مرتب سازی مبتنی بر مقایسه برابرLogn ! یا  nLong است.