بخشی از مقاله
ردیابی حرکت به روش وفقی
چکیده : ردیابی حرکت با روش مش دو بعدی بر مبنای ایجاد یک شبکه مش بر روی تصویر و اجازه تغییر شکل به هر سلول مش در فاصله هر دو فریم متوالی با الزام به پیوستگی مش میباشد. بنابراین این روش بسیاری از اغتشاشات روش بلوکینگ که در جبران حرکت و یا ردیابی حرکت با روش تطبیق بلوک معمول میباشند را به طور مؤثری حذف میکند. در مدلهای مش یکنواخت، الزام به پیوستگی ساختار مش در کل فریم تصویر میباشد، در صورتی که واضح است چنین چیزی در مرزهای همپوشانی اشیاﺀ مناسب نیست. برای فائق آمدن بر چنین محدودیتی، روش مش وفقی که در آن الگوریتمهای شناسایی نواحی ای از پس زمینه که در فریم بعدی پوشانده خواهند شد(-background to be covered (BTBC و نواحی ای که انجام جبران حرکت در مورد آنها نشان دهنده عدم پیوستگی در حرکت است ( model failure-( MF بکار گرفته میشود مورد استفاده قرار میگیرد. در مدل مش یکنواخت، یک مجموعه مشخص از نقاط که در واقع نقاط گوشه سلولهای ساختار مش هستند در کلیه فریمهای دنباله تصاویر ویدئویی دنبال میشوند و واضح است که در نواحی ای که اشیاﺀ با یکدیگر همپوشانی کرده اند و یا بعضی اشیاﺀ در حال خروج از صحنه تصویر و بعضی دیگر در حال ورود به صحنه تصویر هستند، این روش کارایی خود را از دست میدهد. در حالی که در روش مش وفقی، در هر فریم با توجه به نواحی ای که در بالا ذکر شد مجدداﹰ مجموعه نقاط و به تبع ساختار مش باز تعریف میشود. در روش مش وفقی، پیوستگی ساختار مش در نواحی پوشیده شده و پوشیده نشده شکسته میشود. این امر بوسیله عدم قرار دهی نقطه ای در پس زمینه پوشیده شده و باز تعریف ساختار مش در ناحیه MF در هر فریم محقق میگردد. ما الگوریتم طراحی مش بر پایه محتوای هر سلول و انتخاب نقاط برای طراحی مش مث لثی دو بعدی و ردیابی حرکت با روش مش وفقی در حضور همپوشانی ارائه شده توسط Yucel Altunbasak را بهبود داده و سپس یک روش مثلث سازی جدید و همچنین یک الگوریتم جدید برای اطمینان از پیوستگی ساختار مش پس از تخمین بردار حرکت نقاط مش را ارائه میکنیم. از آنجا که این ساختار مش بهبود یافته به صورت وفقی بوده و بر مشخصات هر
سلول استوار میباشد، لذا دیگر لزومی به انتقال کلیه نقاط در هر فریم تصویر وجود ندارد.
مقدمه
مدل مش دو بعدی یک روش ردیابی حرکت است که بر مبنای تغییر شکلهای فضایی در سلولهای ساختار مش و نسبتهای همسایگی بین سلولهای مختلف میباشد. حرکت در این روش از طریق انتقال نقاط گوشه سلولهای ساختار مش ردیابی میس شود که این انتقالها با استفاده از میدان حرکت تخمینی محاسبه میگردند1-2. مشهای دو بعدی را میتوان به مشهای یکنواخت با یک اندازه یکسان برای همه سلولها 3و مشهای غیر یکنواخت مانند مشهای hierarchical و content-based
که اندازه سلولها در آنها با توجه به صحنه تصویر به صورت وفقی تغییر میکند تقسیم کرد 4-5-6
سلولها در مش یکنواخت ممکن است در فریمهای متوالی دنباله تصاویر ویدئویی با یکدیگر همپوشانی داشته باشند. در حالی که یک مش غیر یکنواخت بر روی مرزهای اشیاﺀ وفق داده میشود. علاوه بر این زمانی که بیش از یک نوع حرکت در صحنه تصویر وجود دارد، مش یکنواخت از کارایی کافی برخوردار نیست 8-7
در حقیقت، ردیابی شئ، مشخص کردن تغییرات موقعیت مکانی شئ و دنبال کردن آن در یک دنباله تصاویر ویدئویی با یک هدف خاص میباشد. یک ردیابی موفقیت آمیز به میزان زیادی به نحوه و دقت شناسایی نواحی همپوشانی و نواحی MF و تخمین میدان حرکت در نزدیکی مرزهای اشیاﺀ بستگی دارد. جبران حرکت نیز برای تعیین نقاطی که باید از مجموعه نقاط ساختار مش حذف گردند و مشخص کردن مکان نقاط جدید مورد نیاز است.
در این مقاله، ما یک پروسه ردیابی مش وفقی را بیان میکنیم. در این روش، به هیچ نقطه ای اجازه قرار گیری در نواحی ای از پس زمینه که در فریم بعدی پوشیده خواهد شد ( نواحی ( BTBC داده نخواهد شد و ساختار مش در نواحی MF برای ردیابی متوالی این نواحی
واﮊه های کلیدی مش وفقی، تخمین حرکت، تقریب غپ؟yئپژ، مثلث سازی، جبران حرکت
باز تعریف خواهد شد شکل9
این مقاله شامل بخشهای زیر است: در بخش دوم، ما نخست اصول پایه الگوریتم مش وفقی، تخمین میدان حرکت و شناسایی ناحیه BTBC را بیان میکنیم. سپس تقریب polygon بررسی میشود. پس از آن، ما یک پروسه جدید و کارآمد طراحی مش وفقی که برای طراحی مش ابتدایی بکار میرود را بیان میکنیم. در ادامه، ما یک روش جدید مثلث سازی را ارائه و پیاده سازی میکنیم. بخش سوم شامل تخمین حرکت هر نقطه است که در قسمتهای جبران حرکت و ردیابی مش مورد استفاده قرار میگیرد. در ادامه نیز یک الگوریتم باز تعریف و ردیابی به سمت جلوی مش بیان میشود. نتایج تجربی روی تصاویر ساختگی و تصاویر ساده واقعی نشان دهنده موفقیت الگوریتم ردیابی مش وفقی بیان شده در مقایسه با مش یکنواخت برای ردیابی شئ و در حضور همپوشانی است.
مش وفقی
در این قسمت به اصول پایه الگوریتم مش وفقی پرداخته میس شود.
مفهوم مش وفقی
در مدلهای مش استاندارد، الزام به پیوستگی حرکت در کل فریمها وجود دارد و به روشنی چنین چیزی در مواقعی که حرکتهای چندگانه و نواحی همپوشانی در صحنه تصویر وجود دارد مطلوب نیست ب 1-2 مفهوم مش وفقی نیز برای فائق آمدن بر این محدودیت مهم در ردیابی حرکت بیان شد.
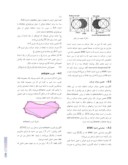
به عنوان مثال، یک شئ بیضی شکل متحرک را مطابق شکل 1 در نظر بگیرید.
uncovered background-UB
شکل: مفهوم مش وفقی
فرض کنید که شئ در حال حرکت به سمت راست است؛ بنابراین دو نوع حرکت در صحنه تصویر وجود خواهد داشت: حرکت به سمت راست که به ناحیه BTBC تخصیص داده میس شود و حرکت به سمت چپ که به ناحیه ای از پس زمینه تخصیص داده میشود که در فریم جاری پوشیده شده است و در فریم بعدی دیگر پوشیده نخواهد بود و به آن ناحیه گفته میشود. توجه کنید که
ناحیه BTBC در فریم k باید کاملاﹰ در فریم1k+ پوشیده شود و ناحیه UB در فریم 1k+ نیز باید کاملاﹰ در فریم k پوشیده باشد.
- تخمین میدان حرکت
الگوریتم تخمین میدان حرکت استفاده شده در این مقاله، بردارهای حرکت را به طور مستقل در هر پیکسل از یک میدان شار نوری یا optical flow با استفاده از روش Horn-Schunck 10تخمین میزند. یک روش تخمین میدان حرکت بر پایه میدان شار نوری بهتر از روشهای دیگر به عنوان مثال روش تطبیق بلوک است زیرا روشهای بر پایه شار نوری میدانهای حرکت یکنواخت تری که برای پارامتری کردن میدان حرکت مناسب تر است ایجاد میکنند 11. در 12 روش دیگری نیز برای تخمین میدان حرکت بر پایه روش split-and-merge توسط Lucas و Kanade بیان شده است.
شناسایی ناحیه BTBC
الگوریتم شناسایی ناحیه BTBC که در [1,2]مورد استفاده قرار گرفته است شامل مراحل زیر میباشد:
1) محاسبه اختلاف فریم دو فریم متوالی و تعیین ناحیه تغییر یافته با استفاده از آستانه گذاری و اعمال پردازشی به صورت
زیر:
الف) فیلتر کردن با استفاده از فیلتر median با اندازه 5×5 .
ب) سه مرتبه استفاده متوالی از عمل مورفولوﮊی closing با اندازه 5×5 و سپس سه مرتبه استفاده متوالی از عمل مورفولوﮊی opening با همان اندازه.
ج) حذف نواحی کوچک که کوچکتر از یک اندازه از پیش تعیین شده برای مثال 25 پیکسل میباشند.
2) تخمین میدان حرکت از فریم k به فریم.k+1
3) جبران حرکت با استفاده از میدان حرکت برای فریم k از
فریم k+1 برای محاسبه فریم مجازی . I~k
- تقریب polygon
زمانی که لازم است مرز یک ناحیه بوسیله یک مجموعه نقاط تقریب زده شود به گونه ای که این مجموعه نقاط باید نزدیکترین تقریب به ناحیه مورد نظر با تعداد محدودی پارامتر را فراهم کند، تقریب polygon میتواند بکار برده شود. این تقریب همانگونه که در شکل 2 مشاهده میشود به طور طبیعی بر مرزهای یک ناحیه منطبق میشود.
شکل2: تقریب polygon
الگوریتم تقریب polygon دارای مراحل زیر است بذ،صذم (13و1)دو پیکسل ( 1و2 ) روی مرز ناحیه که دارای ماکزیمم فاصله از یکدیگر میباشند را بیابید. خط واصل بین این دو نقطه، محور اصلی نامیده میشود.
ل)دو نقطه ( 3و4 ) روی مرز در دو جهت محور اصلی که
دارای بزرگترین فاصله عمودی از محور اصلی هستند را بیابید. این چهار نقطه را نقاط اصلی مینامند.
3)اکنون، چهار قسمت 1-3و2-3و2-4و1-4 وجود دارد. قسمت 3-1 را در نظر بگیرید. یک خط مستقیم از نقطه 1 به نقطه 3ترسیم کنید. هر پیکسل روی مرز که بین 1و 3 قرار دارد و هر پیکسل که در ناحیه بین مرز و خط مستقیم قرار دارد را شناسایی کنید. اگر ماکزیمم فاصله عمودی بین خط مستقیم و هر پیکسل روی مرز کمتر از یک آستانه خاص است و پیکسلهایی که در ناحیه بین مرز و خط مستقیم قرار دارند کمتر از مثلاﹰ 5% کل پیکسلهای ناحیه مورد نظرهستند، آنگاه لازم نیست هیچ نقطه جدیدی در این قسمت از مرز قرار داده شود. اما اگر هر دو شرط فوق با هم محقق نمیشوند، باید یک نقطه جدید روی مرز در محل پیکسل با ماکزیمم فاصله از خط مستقیم قرار داده شود. این پروسه ادامه مییابد تا وقتی که هیچ نقطه جدیدی لازم نباشد در قسمتهای مرزی که جدیداﹰ ایجاد شده اند قرار داده شود.
4)مرحله 3 برای سه قسمت مرزی باقیمانده تکرار میشود. نتایج پیاده سازی الگوریتم فوق برای چندین ناحیه دلخواه در شکل ص نشان داده شده است. معیار توقف الگوریتم را میتوان تعداد ماکزیمم نقاطی که الگوریتم مجاز به قرار دهی روی مرز است قرار داد. اگر تعداد نقاط قرار داده شده روی مرز بیشتر از این تعداد ماکزیمم برای مثال 64 نقطه شود، الگوریتم متوقف میشود؛ اگر چه در عمل معمولاﹰ این تعداد نقطه لازم نمیشود. الگوریتم پیاده سازی شده در اینجا دارای معیار توقف 64نقطه است ولی به آسانی قابل بسط به 128یا 256 نقطه میباشد. از دیگر مزایای الگوریتم پیاده سازی شده، میتوان به عدم وجود هیچ محدودیت خاصی بر روی شکل و اندازه ناحیه تقریب زده شده اشاره کرد.
انتخاب نقاط برای طراحی مش دوبعدی مثلثی
در این قسمت، ما یک الگوریتم جدید و مؤثر انتخاب نقاط را برای طراحی مش دو بعدی مثلثی بیان میکنیم.
این الگوریتم یک مش غیر یکنواخت را ایجاد میکند به گونه ای که چگالی نقاط متناسب با شدت تغییرات محلی حرکت است و مرزهای مش منطبق بر مرز های اشیاﺀ میشود. بنابراین، نقاط باید در روی لبه ها و یا در محل پیکسلهای با بیشترین گرادیان قرار داده شوند. این پروسه در شکل خ نشان داده شده است. دایره های بزرگ نشان دهنده شدت تغییرات کم در اطراف نقطه مورد نظر و دایره های کوچک نشان دهنده شدت تغییرات زیاد در اطراف آن نقطه هستند.
پس از انتخاب نقاط، یک پروسه مثلث سازی با استفاده از نقاط انتخاب شده انجام میشود. الگوریتم دارای مراحل زیر است: ذ)ناحیه شئ را با تقریب polygon تقریب بزنید.
ل)همه پیکسلها به جزﺀ آنها که در ناحیهBTBC قرار دارند را به صورت unmark نشانه گذاری کنید. DFD میانگین را برای همه پیکسلهای unmark با استفاده از رابطه زیر محاسبه کنید:
در رابطه 2، پارامتر k تعداد پیکسلهای unmark است و p میس تواند مقدار 1یا 2 انتخاب شود.
3) یک دایره حول هر نقطه که از تقریب polygon بدست آمده است تا زمانی که در این دایره بزرگتر از DFD میانگین است رشد بدهید. همه پیکسلهای درون این دایره را به صورت marked نشانه گذاری کنید.
4)ناحیه BTBC را نشانه گذاری کنید.
5)یک تابع ارزش برای هر پیکسل unmark با استفاده از رابطه زیر محاسبه کنید:
6)یک پیکسل unmark که دارای بزرگترین مقدار تابع
ارزش ج x, y ض C است را انتخاب کنید و یک ناحیه دایره ای
شکل با یک شعاع از پیش تعریف شده در حول آن در نظر بگیرید . اگر هیچ نقطه marked دیگری در این دایره وجود ندارد، این پیکسل جدید را نشانه گذاری کنید.
7)یک ناحیه دایره ای شکل در حول این پیکسل جدید مشابه مرحله 3 رشد بدهید. زمانی که ناحیه رشد داده شده در حال برخورد با یک ناحیه marked دیگری است، رشد دایره را متوقف کنید حتی اگر شرایط مرحله ص محقق نشده باشد.
8)مرحله 6 را تا زمانی که یک تعداد مطلوب نقطه انتخاب شده باشد تکرار کنید.
شکل5 نتایج پروسه فوق را برای یک مربع که در حال حرکت به سمت راست است نشان میدهد.
شکل 5: :نتایج الگوریتم انتخاب نقاط برای مش دو بعدی
مثلث سازی
ما در این قسمت یک الگوریتم سریع و آسان برای مثلث سازی با نام الگوریتم star-polygon را ابداع کرده و ارائه میس کنیم. این الگوریتم شامل مراحل زیر است:
1)نقطه M از مجموعه نقاط مش را در نظر بگیرید.
2)نزدیکترین نقطه همسایه M که درست در بالای آن قرار دارد را پیدا کنید و در جدول همسایگی M قراردهید.
3)نزدیکترین نقطه همسایه M که درست در پایین آن قرار دارد را پیدا کنید و در جدول همسایگی M قراردهید. شکل 6 را ببینید.
4)صفحه تصویر را بوسیله یک خط عمودی گذرا از نقطه M به دو قسمت تقسیم کنید.
5) همه نقاط نیم صفحه راست را به عنوان همسایگان نقطه M در نظر بگیرید. اگر دو نقطه روی یک خط یکسان گذرا از نقطه M قرار دارند، نقطه ای که به M نزدیکتر است را نگه