بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
Quicksort
Hoare در سال 1962 پيشنهاد كرده است
از روش تقسيم و حل (Divide & Conquer) استفاده مي كند
آرايه را به صورت “در جا” (In P ace)مرتب مي كند
–شبيه مرتب سازي درجي(Insertion Sort) است.
–برخلاف (Merge Sort ) به حافظه اضافي نياز ندارد.
پياده سازي هاي سريعي كه براي آن ارائه شده، باعث بكارگيري وسيع آن در عمل شده است.
اسلاید 2 :
تقسيم و حل
.1تقسيم:يك عضو مثل x از آرايه را انتخاب كرده و آرايه را طوري به دو بخش طوري تقسيم مي كنيم كه يك بخش آن از x كوچكتر و بخش ديگر از x بزرگتر باشند.
.2حل: به صورت بازگشتي هر كدام از اين دو بخش را مرتب مي كنيم
.3تركيب: كارخاصي لازم نيست!
نكته: هزينه عمل تقسيم خطي است Θ(n)
اسلاید 3 :
تقسيم
PARTITION(A, p, q)// A[p. . q]
x←A[p] // pivot= A[p]
i←p
for j←p+ 1 to q
do if A[j] ≤x
then i←i+ 1
swap A[i] ↔A[j]
swap A[p] ↔A[i] // fina p ace of pivot!
return i
اسلاید 4 :
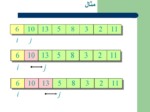
مثال
اسلاید 5 :
شبه كد الگوريتم مرتب سازي
QUICKSORT(A, p, r)
if p< r
then q←PARTITION(A, p, r)
QUICKSORT(A, p, q–1)
QUICKSORT(A, q+1, r)
Initia ca :QUICKSORT(A, 1, n)
اسلاید 6 :
آناليز الگوريتم
فرض كنيد تمام اعضاي آرايه غير تكراري هستند.
در عمل معمولا روشهاي مناسبتري براي تقسيم آرايه هايي كه اعضاي تكراري دارند، استفاده مي شود
فرض كنيد T(n) هزينه مرتب سازي آرايه اي به طول n با استفاده ازاين الگوريتم در بدترين حالت باشد.
معمولا بهترين حالت الگوريتمها را در نظر نمي گيريم اما براي مرتب سازي سريع اين حالت را نيز بررسي مي كنيم.
اسلاید 7 :
بدترين حالات quicksort
آرايه از قبل مرتب شده باشد.
تقسيم حول مقدار مينيمم يا ماكزيمم صورت گيرد.
يكي از دو بخش بدست آمده از تقسيم، هيچ عضوي نداشته باشد.
T(n) = T(0) + T(n-1) + Θ(n)
= Θ(1) + T(n -1) + Θ(n)
= T(n-1) + Θ(n) à n + n-1+ …+1
= Θ(n2)
اسلاید 8 :
درخت هزينه بدترين حالت
اسلاید 9 :
بهترين حالت
در بهترين حالت، دو بخش تقسيم شده تقريبا هم اندازه هستند و اندازه مساله در هر بار تقسيم نصف مي شود:
T(n) = 2T(n/2) + Θ(n) à Θ(n og n) (mergesort)
سوال: اگر تقسيم طوري صورت بگيرد كه 90% اعضاي آرايه در يك بخش و %10 در بخش ديگر قرار بگيرند، هزينه الگوريم چگونه خواهد بود ؟
T(n) = T(n/10) + T(9n/10)+ Θ(n)
اسلاید 10 :
حالتي ديگر
فرض كنيد، به صورت متوالي در هربار تقسيم، آرايه بطور متوازن و نامتوازن تقسيم شود. حالت متوازن را ucky و حالت نا متوازن را un ucky مي ناميم و هزينه الگوريتم را محاسبه مي كنيم
(n) = 2U(n/2) + Θ(n) à ucky step
U(n) = (n -1) + Θ(n) à Un ucky step
(n) = 2( (n/2-1) + Θ(n/2)) + Θ(n)
(n) = 2 (n/2 -1) + Θ(n) à (n) = Θ(n ogn)