بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مرتب سازي مقايسه اي
lتاكنون چندين الگوريتم مرتب سازي را بررسي كرده ايم. در همه اين الگوريتمها، اعضاي آرايه با هم مقايسه مي شوند. اين نوع الگوريتم ها را مقايسه اي مي گوييم.
l بهترين زمان اجراي الگوريتمهاي بررسي شده در بدترين حالت، n log n بوده است.
–Quicksort, Mergesort, Heapsort
lآيا مي توان الگوريتمي با زمان كمتر از n log n ارائه داد؟
lآيا روش ديگري غير از انواع مختلف الگوريتم هاي مقايسه اي؛ براي مرتب سازي وجود دارد ؟
اسلاید 2 :
مساله مرتب سازي
<a1, a2, a3 > ترتيب ممكن:
l<a1, a2, a3>
l<a1, a3, a2>
l<a2, a1, a3>
l<a2, a3, a1>
l<a3, a1, a2>
l<a3, a2, a1>
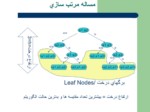
اسلاید 3 :
lدرخت تصميم يك الگوريتم مرتب سازي بايد حداقل n!برگ داشته باشد تا تمام حالات ممكن ترتيب nعدد را در برگيرد.
lبدترين حالت يك الگوريتم ، ارتفاع درخت است.
l درخت دوديي به ارتفاع h حداكثر 2h برگ دارد. اين تعداد برگ بايد تمام ترتيبات مختلف را پوشش دهد.
l2h >= n! à h > log(n!)
ln! ≈ (n/e) n (قضيه استرلينگ)
lh > n log ( n/e)= nlogn –nloge à h = O(nlogn)
lكمترين زمان اجراي الگوريتمهاي مقايسه اي n log n است.
–اين نتيجه نا اميد کننده است ؟
ارتفاع درخت = بيشترين تعداد مقايسه ها و بدترين حالت الگوريتم
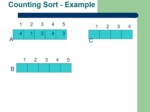
اسلاید 4 :
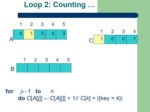
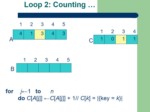
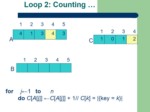
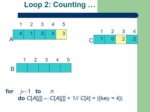
Counting-sort(A[1..n]) //A is an integer array
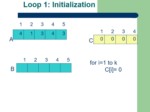
for i←1 to k // k = max(A[1..n])
do C[i] ←0
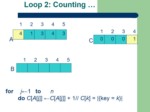
for j←1 to n
do C[A[j]] ←C[A[j]] + 1 //C[i] = |{key = i}|
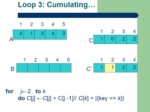
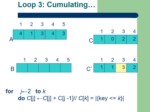
for i←2 to k
do C[i] ←C[i] + C[i–1] //C[i] = |{key ≤i}|
for j←ndownto 1
do B[C[A[j]]] ←A[j]
C[A[j]] ←C[A[j]] –1
اسلاید 5 :
lif k = Θ(n) à T(Countingsort(n))= Θ(n)
lآيا اين نتيجه تناقضي با حداقل بدست آمده در بخش اول دارد؟
–توجه كنيد: در اين الگوريتم هيچ مقايسه اي صورت نمي گيرد!
–نتيجه بدست آمده در بخش اول براي الگوريتم هاي مقايسه اي بود
اسلاید 6 :
- الگوريتم Counting Sort در صورتي كه دو عضو آرايه كليد مساوي داشته باشند، ترتيب آنها را حفظ مي كند. اين نوع الگوريتم را مرتب سازي پايدار مي نامند
اسلاید 7 :
lHerman Hollerith در سال 1890 ، پيشنهاد كرد.
–اين الگوريتم، در محاسبات آماري سال 1890 آمريكا بصورت مكانيكي و الكتريكي پياده سازي و استفاده شد
–نتايج سرشماري دوره قبل 10 سال طول كشيده بود. با استفاده از اين ماشين، گزارشهاي آماري اوليه ظرف 6 هفته! منتشر شد
lاعداد را رقم به رقم و بصورت پايدار مرتب مي كند
lالگوريتم اوليه از پر ارزشترين رقم شروع مي كند
lالگوريتم بهبود يافته از پايين ترين ارزش شروع مي كند
اسلاید 8 :
- اگر با استفاده از اين الگوريتم، دو عدد تا رقم t-1 مرتب شده باشند، با مرتب سازي آنها بر اساس رقم t :
- درصورتي كه رقم t دو عدد يكي باشد، خاصيت پايداري سبب حفظ ترتيب فعلي آنها مي شود.
- در صورتي كه اين دو رقم متفاوت باشند، ارزش بالاي رقم t ترتيب دو عدد را تعيين مي كند.
اسلاید 9 :
lبراي مرتب سازي n عدد دهدهي(Decimal Integer) كه ارقام آنها از 0 تا 9 متغير است، لازم است به تعداد ارقام اعداد (مثلا d) فرايند مرتب سازي تكرار شود.
l با استفاده از Counting Sort بعنوان الگوريتم مرتب سازي ارقام، بسادگي مي توان ديد كه فرايند مرتب سازي هزينه اي برابر Θ(d * (n +k) ) دارد كه در آن k تعداد انواع رقم است(براي اعداد دهدهي ، k=10)
lمي توان اين الگوريتم را طوري تغيير داد كه در هر فاز بيش از يك رقم را مورد استفاده قرار دهد
اسلاید 10 :
lاعداد در كامپيوتر بصورت باينري ذخيره مي شوند و از آنجاكه عملگرهاي مقايسه اي بيتها در سخت افزار بصورت دستورات cpu پياده شده، هوشمندانه است از ارقام دوديي براي مرتب سازي استفاده شود
lهنگام استفاده از اعداد باينري، معمولا بيش از 1 بيت بعنوان يك رقم استفاده مي شود.
–اگر اعداد 32 بيتي را با رقم 4 بيتي مرتب كنيم، 8 بار لازم است فرايند مرتب سازي رو ي ارقام مختلف اجرا شود. Counting Sort 24 يا 16 عدد مختلف را مرتب مي كند