بخشی از پاورپوینت
اسلاید 1 :
ارائه دوالگوريتم براي ادغام دو ليست مرتب
الگوريتم غير بازگشتي Merge Sort
الگوريتم بازگشتي Merge Sort
اسلاید 2 :
Merge Sort يكي از روش هاي مرتب سازي داخلي است.
در مرتب سازي به روش ادغام آرايه يا ليست مورد نظر طي چند مرحله به تعدادي آرايه يا ليست تك عضوي شكسته مي شود.
نكات:تعداد آرايه ها يا ليست هاي تك عضوي همان تعداد اوليه ي نودها يا اعضاي آرايه هستند .
طول ليست يا آرايه ي اوليه را Nدر نظر بگيريد.
به جاي آرايه ليست به كار مي بريم .
اسلاید 3 :
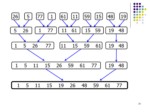
بعد از شكستن ليست،زيرليست ها را با هم ادغام مي كنيم و
زيرليست هاي مرتب ديگري بدست مي آوريم .
زير ليست هاي مرتب را طي چند مرحله با هم ادغام مي كنيم تا به يك ليست مرتب با N عضو برسيم.
اسلاید 4 :
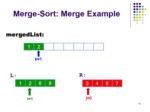
ادغام دو ليست مرتب:
Init ist[ ],…,init ist[m] init ist[m+1],…,init ist[n]
دو ليست مرتب شده از نوع E ementهستند، به طوري كه:
Init ist [ ].key≤…≤ init ist [m].key
Init ist[m+1].key ≤…≤ init ist [n].key
در تابع Mergeاين دو ليست مرتب با يكديگر ادغام مي شوندو
تابع مرتب شده ي جديدي به نام Merged ist ايجاد مي شود.
اسلاید 5 :
Merge A gorithm:
void merge(E ement *init ist,E ement *merged ist,
const int,constint m,constint n)
{
for(int i1= ,iResu t= ,i2=m+1;i1<=m&&i2<=n; iResu t ++)
if(init ist[i1].getkey()<=init idt[i2].getkey()) {
merged ist[iResu t]=init ist[i1];
i1++;
e se {
merged ist[iResu t]=init ist[i2];
i2++;
if(i1>m)
for(int t=i2;t<=n;t++)
merged ist[iResu t+t-i2]=init ist[t];
e se
for(int t=i1;t<=m;t++)
merged ist[iResu t+t-i1]=init ist[t];
اسلاید 6 :
از آنجا كه مرتب سازي ادغام شامل چند مرحله است از اين رو بهتر است ابتدا تابعي براي اين منظور معرفي كنيم:
MergePass Function
پس از آن به معرفي MergeSort A gorithm مي پردازيم كه مرتب سازي را با احضار مكررتابع Merge Pass انجام مي دهد.
اسلاید 7 :
MergePass A gorithm
VoidMergePass(E ement *init ist, E ement *resu t ist ,const int n ,const int )
{
for ( int i=1 ; i<=n-2* +1 ; i+=2* )
merge ( init ist , resu t ist , i , i+ -1 , i+2* -1 );
i=1< 3 i=3<=3
n=4 =1 i<=3
n=4 =2 i<=1
اسلاید 8 :
MergePass A gorithm
VoidMergePass(E ement *init ist, E ement *resu t ist ,const int n ,const int )
{
for ( int i=1 ; i<=n-2* +1 ; i+=2* )
merge ( init ist , resu t ist , i , i+ -1 , i+2* -1 );
if ( ( i+ -1) < n)
merge ( init ist , resu t ist , i , i+ -1 , n);
e se
for ( int t=i ; t<=n ; t++ )
resu t ist[t]=init ist[t];
اسلاید 9 :
MergeSort A gorithm
Void MergeSort ( E ement * ist , const int n )
{
E ement * temp ist= new E ement [n+1];
// is the ength of the sub ist current y being merged
for ( int =1 ; <n ; *=2 )
{
MergePass ( ist , temp ist , n , );
*=2;
MergePass ( temp ist , ist , n , ); // interchange ro e of ist and temp ist
De ete [ ] temp ist;
اسلاید 10 :
تجزیه و تحلیل تابع MergeSort :
تابعMergeSort در چند مرحله از رکوردهای مرتب شونده عبور می کند.در مرحله ی اول لیست هایی به طول 1 ادغام می شوند.مرحله ی دوم طول لیست های ادغام شونده 2 است .درمرحله ی i ام لیست های ادغام شونده طول 2i-1 دارند.
در نتیجه تعداد کل مراحل عبور از داده ها og2n ] [ است.
هر مرحله از مرتب سازی ادغام در زمان O(n) انجام می شود و زمان اجرای کل O(n ogn) است.