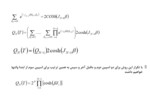بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
پديدة گذار فاز
پديدهاي است كه با بروز يك ناپيوستگي در ترموديناميك يك دستگاه همراه است.
گذار فاز مرتبة اول:
مشتق اول پتانسيل گيبس در عبور از مرز فاز گسسته است.
گذار فاز مرتبة دوم و بالاتر:
در اين گذار ها سيستم بدون تغيير حالت يک شکست تقارن دارد.
مثل تبديل مواد پا رامغناطيس به مواد فرو مغناطيس در اين حالت پارامتر نظم است و بدون اينكه سيستم تغيير حالت پيدا كند سيستم تقارنش را نسبت به دوران از دست ميدهد.
اسلاید 2 :
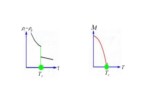
پديدة فرو مغناطيس
- در بعضي از فلزات كسري از اسپين اتمها در دماي پايينتر از دماي خاصي (دماي بحراني) در يك جهت خاص تطبيده ميشوند و يك ميدان مغناطيسي خود بخودي ايجاد ميكنند.
مطالعة اساسي در گذار فاز مطالعه رفتار سيستم در همسايگي نقطة بحراني است.
اسلاید 3 :
مدل آيزينگ
هر جا كه با زنجيري از يك خصوصيت و يا با انتشاري كه همسايگي در آن نقش مهمي داشته باشد مدل آيزينگ را ميتوان آزمود. مثلاً بررسي يك بيماري مسري و انتشار آن در يك جامعه و يا ارتباط شركتهاي تجاري و همچنين در موقعيتهايي كه پارامتر يا كميت خاصي از سيستم دو انتخاب براي مقدار گيري داشته باشد يا بتوان تعداد اين انتخابها را به دو مقدار تقليل داد.
اسلاید 4 :
مدل آيزينگ در گذار پارامغناطيس- فرو مغناطيس
براي حل سيستمهاي شيميايي- فيزيكي كه دستخوش انتقال فاز ميشوند بوسيلة آرايش شبكهاي كه فقط نيروهاي بر هم كنشي اتمهايي كه در همسايگي هم هستند را در نظر ميگيريم كه نحوة آرايش (اشغال فضا) اين برهم كنشها را تغيير ميدهد اين مدل خواص ترموديناميكي پديدهها را تغيير نميدهد. مدل آيزينگ تلاشي است براي شبيهسازي ساختار يك جسم فرومغناطيس و مزيت اصلي آن اينست كه اين مدل در دو بعد به بررسي دقيق در مكانيك آماري منجر ميشود.
اسلاید 5 :
در اين مدل سيستم به صورت آرايهاي از N نقطة ثابت كه جايگاههاي شبكه ناميده ميشود و در نظر گرفته ميشود. اين آرايه شبكه n بعدي را تشكيل ميدهد كه يك متغيير اسپيني به هر جايگاه شبكه نسبت داده ميشود كه عددي برابر 1+ يا 1- است.
معرف يك پيكربندي است.
شكل يك نمونهاي از يك پيكربندي براي سيستمي با 5 جايگاه است كه پيكربندي اين شكل {1-، 1+، 1+، 1-، 1+}={δ1}است.
اسلاید 6 :
انرژي سيستم در يك پيكره بندي {δi }
جملة اول ناشي از بر هم كنش اسپيني نزديكترين همسايه است كه در اين رابطه J ثابت جفت شدگي يا متبادلي نام دارد كه تابعي از فاصلة بين دو اسپين است. فرض ميكنيم كه J به مكان ذرة i و j بستگي نداشته باشد.
n.n معرف نزديكترين همسايههاي هر جايگاه است و q تعداد اين همسايهها، هندسه شبكه از طريق J , q وارد مسأله ميشود.
جمله دوم ميانگين برهم كنش تك تك اسپينها با ميدان مغناطيسي است.
اسلاید 7 :
بررسي مدل آيزينگ در يك بعد
با استفاده از خاصيت تبادلي شبكه بلوري ما ميتوانيم ساختار بسته و متناهي را جايگزين شبكه متناوب بكنيم. بنابراين ساختار مربوط به شبكه يك بعدي منحني بستهاي است كه N امين عضو شبكه در كنار اولين اسپين قرار ميگيرد.
اسلاید 8 :
بررسي مدل آيزينگ در يك بعد
تابع پارش سيستم
اسلاید 9 :
محاسبه كميتهاي ترموديناميكي سيستم و دماي گذار
اسلاید 10 :
در غياب ميدان مغناطيسي، مغناطش سيستم صفر است البته اين در شرايطي است كه سيستم به دماي گذار و پس از آن نرسيده باشد در آن صورت ما مغناطش خودبخودي خواهيم داشت.