دانلود پاورپوینت تئوری بازیها

بخشی از پاورپوینت

اسلاید 1 :

تئوريبازي ها 

بازيها چه هستند و چرا مطالعه ميشوند؟

بازي ها: حالتي از محيطهاي چند عاملي را نشان مي دهند که:

þ هر عامل نياز به در نظر گرفتن ساير عاملها و چگونگيتأثير آنها دارد

þ تمايزبينمحيطهايچند عامل رقابتيو همکار

þ محيطهايرقابتي، که در آنها اهداف عاملها با يکديگربرخورد دارند، منجر به مسئله هايرقابتيميشود که به عنوان بازي شناخته ميشوند

اسلاید 2 :

و چرا بازي ها مطالعه مي شوند :

× قابليتهايهوشمندي انسانها را به کار ميگيرند

×ماهيتانتزاعيبازي ها

×حالت بازي را به راحتيميتواننمايش داد و عاملها معمولا به مجموعه کوچکي از فعاليتها محدود هستند که نتايج آنها با قوانيندقيقيتعريف شده اند

به عنوان مثال: دلايلي که محققين قديم، شطرنج را به‌عنوان موضوعي در AI برگزيدند:

ï بازي شطرنج کامپيوتري اثباتي بر وجود ماشيني است که اعمال هوشمندانه‌اي را انجام مي‌دهند.

ï سادگي قوانين

ï وضعيت دنيا کاملاً براي برنامه شناخته شده است. (بازنمايي بازي به عنوان يک جستجو از طريق فضاي موقعيت‌هاي ممکن بازي، ساده است.)

اسلاید 3 :

 پيچيدگي بازي‌ها، به طور کامل نوعي از عدم قطعيت را معرفي مي‌کنند.

عدم قطعيت به علت وجود اطلاعات گم شده رخ نمي‌دهد، بلکهبه علت اينکه فرد زماني براي محاسبه دقيق نتايج حرکت ندارد عدم قطعيت بوجود مي‌آيد.

در اين مورد، فرد بر اساس تجربيات گذشته مي‌تواند بهترين حدس را بزند.

اسلاید 4 :

يک نمونه بازي

- يک بازي با دو بازيکن را در نظر مي‌گيريم که آن را MIN-MAX  مي‌ناميم.

- بدين معناست که هر يک از بازيکن ها ، حرکت خود را در جهت افزايش برد خود (max) و نيز در جهت کاهش برد حريف (min) انجام مي دهد.

- پس هميشه حرکت با max است. قبل از حرکت گرافي از ديد بازيکن max رسم مي شود که بتواند بهترين حرکت را انتخاب کند:

×حالت اوليه: موقعيت صفحه و شناسايي حرکت مجاز

×عملگرها: ليستي از (حالت,حرکت) که معرف يک حرکت معتبر است

×آزمون هدف: پايانبازي چه موقع است؟ (حالتهايپايانه)

×تابع سودمندي: براي هر حالت پايانهيک مقدار عددي را ارائه ميکند.            مثلاً: برنده(1+) و بازنده(1-) و مساوي(0)

اسلاید 5 :

الگوريتم  :MIN-MAX

به منظور تعيين استراتژي بهينه براي MAX طراحي شده است و از اينرو مي‌توان بهترين حرکت را تصميم‌‌گيري کرد. الگوريتم شامل 5 مرحله است:

.1توليد درخت کامل بازي، تمام راه تا مراحل پاياني

.2درخواست تابع سودمندي براي هر حالت پاياني به منظور بدست آوردن مقدارش.

.3از سودمندي حالات پاياني به منظور تعيين سودمنديگره‌ها يک مرحله بالاتر دردرخت جستجو استفاده کنيد.

.4بررسي مقادير را از گره‌هاي برگي تا ريشه، يک لايه در هر لحظه، ادامه دهيد.

.5احتمالاً مقادير به بالاي درخت مي‌رسند، MAX حرکتي را انتخاب مي‌کند که به بالاترين مقدار منتهي مي‌شود.

اسلاید 6 :

m: حداکثر عمق درخت،

b: تعداد حرکات قانوني در هر نقطه،

þ کامل بودن: بله (اگر درخت محدود باشد)

þ پيچيدگيزماني:الگوريتمminimax، O(bm) است.              الگوريتم يک جستجو عمقي است.

اسلاید 7 :

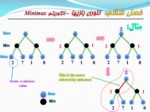
بازيهاي قطعي با اطلاعات ناقص (ترسيم درخت بطور ناقص):

بهتريننتيجه ممکنه برايبازيکني است که گراف را کامل کرده است . استراتژيبازي براساس مسيرهايي از گراف که بهتريننتيجه را مي دهد، تعريفمي شوند

اينتئوري در عمل برايبازيهايي که گراف آنها بسيارپرهزينه است استفاده نمي شود. براي مثال در بازي شطرنج:

ميانگين فاکتور انشعاب در حدود 35

در اغلب بازيها هر بازيکن تا 50 حرکت

پس اگر بخواهيم به اينتئوري جنبه عمل دهيمبايدسعيکنيم براساس گراف کوچک که بخشي از گرافاصلي محسوب مي شود استراتژي را تعيين کرد.

اسلاید 8 :

الگوريتمMinimax  به دو راه تغيير يابد:

q تابع سودمندي با تابع ارزيابياکتشافيEVALجايگزين شود.

  - تخميني از سودمنديموقعيت ارائه ميکند

q آزمون پاياني با آزمون قطع Coutoff testجايگزين گردد.

             - تصميمميگيردEVAL چه موقع اعمال شود

اسلاید 9 :

Evaluation Function 

- واضح است که ارائه يک برنامه بازي بي نهايت به کيفيت تابع ارزيابي بستگي دارد.

Ãتابع ارزيابينميداند کدام حالت منجر به چه چيزيميشود، اما ميتواندمقداري برگرداند که تناسب حالتها را با هر نتيجه را نشان دهد

اسلاید 10 :

چگونه به طور دقيق کيفيت تابع ارزياب را مي‌توان اندازه گرفت؟

.1تابع ارزيابي با تابع سودمندي در مورد حالت پاياني بايد به توافق برسند.

.2 نبايد زياد طول بکشد! (اگرپيچيدگي را محدود نکنيم minimax به عنوان يک زيربرنامه فراخواني مي‌شود و مقدار دقيق وضعيت محاسبه مي‌شود.) از اين رو، معامله‌اي بين صحت تابع ارزيابي وهزينه زمان آن وجود دارد.

.3 تابع ارزيابي بايد به درستي شانس‌هاي واقعي براي برد را منعکس کند.