بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
vفرمولاسيون مسائل انتقال حرارت
vروشهای حل تقريبی
vروشهای حل دقيق (تحليلی)
اسلاید 2 :
vانتقال حرارت هدايتی و قانون فوريه (Conduction)
vانتقال حرارت جابجايی (Convection)
vانتقال حرارت تشعشعی (Radiation)
اسلاید 3 :
ديواره ای با ضخامت L را مانند شکل در نظر بگيريدکه يک سمت آن در دمای T0 و طرف ديگر آن در دمای T1 قرار دارد:
توزيع دما براي اين صفحه جامد در حالت يکنواخت (Steady State) که دما با زمان تغيير نمی کند، خطی بوده و حرارت منتقل شده متناسب با اختلاف دما می باشد:
اسلاید 4 :
vدر حالت جامد اتفاق نمی افتد.
vاغلب مکانيزم غالب در سيالات می باشد.
vدر هنگام مدلسازی از قانون سرمايش نيوتن که بصورت زير است، استفاده مي شود:
که در اين رابطه q شار حرارت عبوری، h ضريب انتقال حرارت جابجايی، A مساحت تماس بين فاز جامد با سيال، Ts دمای سطحی که سيال در روی آن قرار گرفته و جمله ی آخر دمای توده سيال می باشد.
اسلاید 5 :
vدر هر سه حالت ماده اتفاق می افتد.
vاغلب مکانيزم غالب در دماهای بالا می باشد.
vدر هنگام مدلسازی از قانون استفان بولتزمن که بصورت زير است، استفاده می شود:
که در اين رابطه q شار حرارت عبوری، σ ضريب استفان – بولتزمن، ε ضريب نشر يا (Emissivity) و A مساحت جسم می باشد.
اسلاید 6 :
vفرمولاسيون مسايل انتقال حرارت مراحل مختلفی دارد که در مثال های زير بدانها اشاره می شود.
اسلاید 7 :
مثال
کره ای به شعاع R0 در اوليه دمای T0 قرار دارد. آنرا در معرض محيط کنوکسيونی با ضريب انتقال حرارت h و دمای T1 قرار می دهيم تا سرد شود. تغييرات دما را در اين کره بدست آوريد.
اسلاید 8 :
1- شناخت دقيق سيستم مانند حدود ابعاد، دامنه بزرگی پارامتر ها و ... .
فرض کنيد که کليه مشخصات اين کره از قبيل طول شعاع، مقدار دمای اوليه و ... مشخص می باشد.
2- شناخت دقيق خصوصيات فيزيکي و ترموفيزيکي مثل چگالي، K، Cp، ويسکوزيته و ... .
فرض کنيد که کليه مشخصات ترموفيزيکی از قبيل K، Cp، h و... برای اين سيستم مشخص می باشد.
اسلاید 9 :
الف) متغير های مستقل همواره مولفه های مکانی مثل x،y و z .... و زمان می باشند.
ب) متغيرهای غير مستقل کليه خصوصيات فيزيکی مثل غلظت، سرعت، فشار، ... می باشند که در مسائل حرارت، متغير غير مستقل همواره دما می باشد.
اسلاید 10 :
در مثال فوق تغييرات دما وابسته به نقاط مختلف کره در زمان های مختلف است. يعنی داريم:
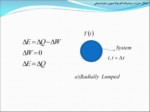
بديهی است که اگر شعاع اين کره يعنی R0 خيلی کوچک باشد، می توان دمای نقاط مختلف کره را در هر لحظه يکسان فرض نمود و از تغييرات دما در شعاع های مختلف صرفنظر کرد. در اين حالت داريم:
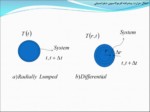
در اين حالت که جهت شعاع از تغييرات دما حذف شده است، مسئله را اصطلاحا در جهت شعاعي Lumped مي ناميم (Radially Lumped).
اين مثال را در دو حالت Lumped و Differential فرموله خواهيم کرد.