دانلود فایل پاورپوینت تحلیل الگوریتم ها ( تحلیل در زبان متلب )

بخشی از پاورپوینت

--- پاورپوینت شامل تصاویر میباشد ----

اسلاید 1 :

عبارت است از

—تعداد دفعاتی که عمل اصلی به ازای هر مقدار از اندازه ورودی انجام می‌شود.

—انتخاب عمل اصلی بر اساس تجربه صورت می‌پذیرد

—

1) پیچیدگی زمانی الگوریتم در حالت معمول

مانند ضرب ماتریس: Cm×k=Am×n×Bn×k

T(m,n,k)=m×n×k

و یا برای سادگی میگوییم: T(n)=n3

اسلاید 2 :

2) پیچیدگی زمانی الگوریتم در بدترین حالت

مانند جستجوی ترتیبی

W(n)=n

3) پیچیدگی زمانی الگوریتم در بهترین حالت

مانند جستجوی ترتیبی

B(n)=1

اسلاید 3 :

4) پیچیدگی زمانی الگوریتم در حالت میانگین

توجه: یک مقدار میانگین را فقط زمانی می‌توان معمولی خواند که حالتهای واقعی از میانگین انحراف زیادی نداشته باشد.

مثال: جستجوی ترتیبی

حالت 1: x همواره در آرایه هست

اسلاید 4 :

در تحلیل پیچیدگی الگوریتم‌ها، پیچیدگی حافظه نیز قابل بحث است

اسلاید 5 :

در بسیاری از موارد نیاز است تا دو الگوریتم را با هم مقایسه کنیم ...

تابع پیچیدگی آنها را (زمانی/حافظه) را بدست می‌آوریم ولی ....

از آنجایی‌که داشتن درک صحیحی از مقایسه دو تابع پیچیدگی در بسیاری از موارد مشکل است، ...

نیاز است تا توابع پیچیدگی را به شکل‌های ساده‌تری بیان کنیم.

از این رو است که بیان پیچیدگی الگوریتم‌ها با مرتبه پیچیدگی که شکل ساده‌ای از توابع پیچیدگی است، کار مقایسه دو الگوریم را

آسان می‌کند.

همچنین ...

اسلاید 6 :

در پاره‌ای از موارد رسیدن به تابع پیچیدگی با داشتن الگوریتم کار پیچیده‌ای است ولی ...

می‌توانیم شکل ساده‌ای از آن را که بیان کننده پیچیدگی مساله باشد را بدست آوریم.

اسلاید 7 :

تعریف Ω  (Omega)

برای یک تابع پیچیدگی مفروض f(n) ، مانند n، log n

 مجموعه‌ای از توابع پیچیدگی g(n) است که برای آنها

به ازای یک ثابت حقیقی مثبت c

آنگاه یک عدد صحیح غیر منفی N وجود دارد

به قسمی که به ازای همه  n≥N داریم g(n) ≥c×f(n)

روش نمایش: g(n) ϵ Ω(f(n)

—

اسلاید 8 :

تعریف Θ (Theta)

برای یک تابع پیچیدگی مفروض f(n) ، مانند n، log n

 مجموعه‌ای از توابع پیچیدگی g(n) است که برای آنها

به ازای ثابت‌های حقیقی مثبت c و d

آنگاه یک عدد صحیح غیر منفی N وجود دارد

به قسمی که به ازای همه  n≥N داریم:

 d×f(n) ≥g(n) ≥c×f(n)

روش نمایش: g(n) ϵ Θ(f(n))

—

اسلاید 9 :

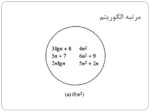
ویژگیهای O:

1- اگر g(n) بتواند به صورت مجموع تعداد محدودی از توابع دیگر نوشته شود، در این صورت آن تابعی که بیشترین رشد را دارد، O را مشخص می‌کند

اسلاید 10 :

ادامه ویژگیهای O:

5- می‌توان O را در بیان پیچیدگی محاسباتی نیز آورد

مثلا T(n)=O(n2)+55n3+2n+10

در این الگوریتم ابتدا مرتب‌سازی انجام می‌پذیرد و سپس کار ادامه می‌یابد