بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مختصات قطبی (r,ө) در مقایسه با مختصات دکارتی (x,y) با معادلات زیر نمایش داده می شود:
r فاصله از مبدا
ө زاویه با قسمت مثبت محور xها
اسلاید 2 :
مختصات استوانه ای تعمیم مختصات قطبی در صفحه 2-بعدی به فضای 3-بعدی است.
نقطه P در این مختصات با سه تایی
مرتب نمایش داده می شود.
اسلاید 3 :
با توجه به شکل تبدیل از مختصات دکارتی به مختصات استوانه ای با معادلات زیر انجام می شود:
اسلاید 4 :
مثال1:
مختصات نقطه (x,y,z)=(1, ,2) را در مختصات استوانه ای بنویسید.
حل: داریم
اسلاید 5 :
یک سیستم مختصات بسیار مفید دیگر در فضای 3بعدی، سیستم مختصات کروی می باشد.
- این سیستم محاسبه انتگرالهای سه گانه محدود به نواحی مخروطی شکل را ساده می کند.
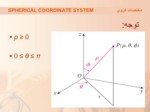
اسلاید 6 :
در زیر مکان هندسی نقطه Pدر فضا با سیستم مختصات کروی(ρ, θ, Φ) نشان داده شده است.
- ρ = |OP| فاصله نقطه Pاز مبدا مختصات
- θ همان زاویه مشابه در سیستم
مختصات استوانه ای
- Φ زاوی بین محور Z ها
و بردار OP
اسلاید 7 :
برای مثال معادله کره ای به مرکز مبدا و شعاع c در سیستم مختصات کروی به صورت زیر در می آید.
- این علت نامگذاری
این سیستم است
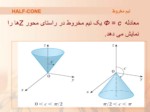
اسلاید 8 :
معادله Φ = c یک نیم مخروط در راستای محور Zها را نمایش می دهد.
اسلاید 9 :
رابطه بین سیستم مختصات کروی و دکارتی در شکل زیر قابل مشاهده است.
اسلاید 10 :
مثال1:
نقطه(2, π/4, π/3) در مختصات کروی داده شده است. آن را در فضای 3-بعدی نمایش داده و مختصات دکارتی آن را بدست آورید.