بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مقدمه
- اولین نشانه ها از تفکر فازی: بودا در 500 پیش از میلاد
تفکر خلاف زایی در دین بودایی: هر عنصری با بوجود آمدن کمی از متضاد خود را نیز در بر دارد.
1 – A != A
- 200 سال بعد: ایجاد تفکر باینری توسط ارسطو
اقبال در میان دانشمندان
حمایت کلیسا
پایه ای برای علوم
- تلاش های راسل برای کاهش ریاضیات به منطق
پارادوکس راسل
- 1964: لطفی عسکرزاده
اسلاید 2 :
- 1964: لطفی عسکرزاده
دستگاه تهویه مطبوع هوش مند
تولد مفهوم فازی بودن
- عدم استقبال خوب در آمریکا و اروپا
- سفر فازی به شرق دور
تطبیق فازی با ادیان شرقی
1987: سامانه ی کنترل اتوماتیک مترو در ژاپن
اولین موفقیت بزرگ
بحث در جوامع علمی و صنعتی دنیا
اسلاید 3 :
- فازی چه می گوید؟
A می تواند با !A برابری باشد!!!
معیاری برای سنجش A بودن لازم است
- تفاوت دیدگاه باینری و فازی:
- یک معیار بهینه تر:
اسلاید 4 :
- موفق ترین راهکار و فنآوری برای طراحی سامانه های خبره
- شبیه سازی تصمیم گیری انسانی
- قابلیت ارائه ی پاسخ های دقیق بر مبنای داده های قطعی یا ناهموار
- تطبیق ابهام دنیای زبان انسانی با منطق ریاضی
- . . .
- اولین کاربردها:
کنترل پروسه های کوره های سیمان
در 1987، اولین بزرگراه کنترل با منطق فازی در Sendai در شمال ژاپن
در آسانسورها برای کاهش زمان انتظار
- کاربردهای کنونی:
ماشین های ظرف شویی، اتومبیل ها، مایکروفرها، . . .
اسلاید 5 :
منطق های دو و چند مقداری
- منطق ارسطویی:
دو مقدار ارزشی، درست یا غلط
پدر منطق های دوارزشی، نظیر منطق مورد استفاده در استنتاج Bayesian و سایر مدل های احتمالاتی
- مشکل:
معمولاً نمیتوان به یقین گفت که یک گزاره در کدام ارزش شکل صحیح تری دارد.
استفاده از احتمالات برای محاسبه ی میزان درست نمایی(Likelihood)
- اولین منطق چند ارزشی توسط Lukasiewicz و Knuth:
فیزیک کوانتوم
منطق سه ارزشی، درست یا غلط یا نامعین
اسلاید 6 :
- گسترش منطق سه ارزشی:
صفر برای نمایش عدم صحت قطعی
یک برای نمایش صحت قطعی
مقادیر بین صفر و یک برای میزان (عدم) صحت غیر قطعی
- تفاوت با احتمالات:
احتمال صحت 0.5بدین معنی است که گزاره احتمال صحتی برابر 0.5 دارد، ولی یا می تواند درست باشد و یا غلط؛ و نه چیزی بین آن ها و نه هر دو و نه هیچ کدام(!!!!!)
اسلاید 7 :
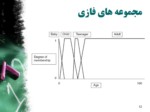
متغییرهای زبانی
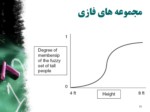
- یک مفهوم، نظیر ارتفاع
- که می تواند مقداری از میان مجموعه مقادیر فازی
- نظیر {بلند، کوتاه، متوسط}
- را بپذیرد.
- متغییرهای زبانی روی یک Universe of Discourse
- نظیر {مقادیر بین 0.8 متر تا 2.5 متر}
- تعریف می شوند.
- مجموعه مقادیر فازی، زیرمجموعه هایی از این دنیا می باشند.
اسلاید 8 :
مجموعه های فازی
- نقطه ی مقابل مجموعه های Crisp:
عدد 0.2 عضوی از مجموعه ی اعداد طبیعی نیست
- چند پرسش:
آیا یک فرد دو متری بلند قد است؟
یک فرد یک متر و نود سانتیمتری چطور؟
یک فرد یک متر و هفتاد سانتیمتری چطور؟
یک فرد یک متر و پنجاه سانتیمتری چطور؟
- مطابق منطق فازی، تمام افراد بالا بلند قد هستند،
- ولی درجه ی بلندقدی شان متفاوت است!
اسلاید 9 :
توابع عضویت فازی
- هر مجموعه ی فازی را با تابع عضویت اش می شناسیم:
- برای نمایش مجموعه ی A داریم:
اسلاید 10 :
- برای مثال سن خواهیم داشت: