بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
تابع خطی
هر تابع که بتوان آن را به شکل خط y=ax+b نمایش داد یک تابع خطی نامیده می شود
این توابع یک به یک هستند و معکوس پذیرند . دامنه و برد آن ها R است. البته باید دقت کنیم که ممکن است یک تابع خطی بخشی از یک تابع باشد. در این صورت دامنه و برد توابع همه ی مجموعه اعداد حقیقی نخواهد بود.
اسلاید 2 :
تابع همانی
اگر دامنه و برد یک تابع برابر باشند و هر عضو در دامنه دقیقاً به همان عضو در برد نظیر شود آن تابع را همانی گویند.
تابع ثابت
تابعی است که برد آن تنها شامل یک عضو است و نمودار آن در صورتی که دامنه آن مشخص نشده باشد خطی است موازی محور x ها و دامنه تمام اعداد حقیقی است .
اسلاید 3 :
تابع درجه 2 ( سهمی )
توابع با ضابطه تابع درجه 2 می گوییم و نمودار آن سهمی است برای رسم ابتدا معادله را به صورت
تبدیل می کنیم سپس آن را با توجه به نکات زیر رسم می کنیم
1- راس سهمی در نقطه قرار دارد و نمودار نسبت به خط قرینه است
2- اگر a>0 نمودار به طرف بالا و در صورتی که a<0 باشد نمودار به طرف پایین باز می شود
در صورتی که دامنه این نوع توابع داده نشده باشد یک به یک نیستند لذا وارون پذیر نیز نیستند. دامنه و برد توابع طوری است که باید تابع را رسم کنیم.
اسلاید 4 :
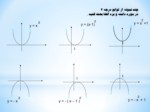
چند نمونه از توابع درجه 2
در مورد دامنه و برد آنها بحث کنید .
اسلاید 5 :
تابع قدر مطلقی
تابعی که هر مقدار دامنه را به قدر مطلق آن نظیر کند تابع قدر مطلق نامیده می شود. تابع قدر مطلق را با f(x)=\x\ نمایش می دهیم. این توابع یک به یک نیستند پس وارون پذیر هم نیستند.
نکته : در حالت کلی در توابع قدرمطلقی داریم :
1- در صورتی که a مثبت باشد نمودار به صورت V و اگر a منفی باشد نمودار به صورت می باشد
2- راس نمودار در نقطه (b,c ) است
اسلاید 6 :
چند نمونه از توابع قدر مطلقی
به نظر شما در رسم این توابع از چه قواعدی استفاده شده است ؟
اسلاید 7 :
تابع رادیکالی
در صورتی به تابعی تابع رادیکالی گفته می شود که متغیر زیر رادیکال رود.
تشخیص دامنه ی این توابع به دو صورت است :
الف) اگر فرجه رادیکال زوج باشد باید زیر رادیکال را بزرگتر مساوی با صفر قرار دهیم.و نامعادله حاصل را حل کنیم .
اسلاید 8 :
مثال : دامنه و برد تابع زیر را به دست آورید
ب) اگر فرجه رادیکال فرد باشد رادیکال را در نظر نگرفته ، دامنه ی تابع با دامنه ی عبارت زیر رادیکال برابر است.
اسلاید 9 :
چند نمودار دیگر این بار از توابع رادیکالی آیا همان قوانین انتقال ها ی توابع قدر مطلقی در این جا هم صادق هستند . در مورد دامنه و برد چه باید بگوییم ؟
اسلاید 10 :
مثال : دامنه تابع زیر را به دست آورید.
توضیح : در این تابع عبارت داخل رادیکال مربع کامل است پس آن را می توان به صورت زیر نوشت :
بنابراین دامنه و برد آن با توجه به شکل آن به صورت زیر است .
دامنه و برد است