دانلود پاورپوینت نمایش مجموعه ها با درخت

بخشی از پاورپوینت

اسلاید 1 :

   مجموعه

Øبه دسته اي از اشيا که در يک يا چند خصوصيت مشترک هستند .

Øمجموعه مجزا :
اگر sj , si دو مجموعه باشند وi≠j باشد ، آن گاه   هيچ عضو مشترکي بين اين دو مجموعه وجود ندارد.

اسلاید 2 :

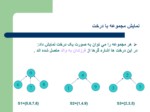
مثال

به عنوان مثال عناصر0 تا 9 را مي توان به سه مجموعه مجزاي زير تفكيك کرد:

l

       S1={0,6,7,8}              

       S2={1,4,9}            

       S3={2,3,5}            

اسلاید 3 :

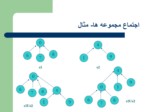
نمايش مجموعه با درخت

Øهر مجموعه را مي توان به صورت يک درخت نمايش داد:

در اين درخت ها اشاره گرها ازفرزندان به والد متصل شده اند .

اسلاید 4 :

نمايش مجموعه ها  …

Ø ابتدا گره هاي درخت را با يك آرايه بهنام Parent[Maxsize] نشان مي دهيم.

Øi امين عنصر اين آرايه  نشان دهنده گره i درخت است.

اسلاید 5 :

عملكردهاي روي مجموعه ها

.1اجتماع دو مجموعه مجزا(Union(i,j))

.2عضويت i در يک مجموعه(Find(i))

اسلاید 6 :

اجتماع مجموعه ها

ØاگرSi,Sj دو مجموعه مجزا باشند ، آن گاه اجتماع آن ها به صورت زير تعريف مي شود :

}     همه عناصر X به صورتي که X يا عضو Si  باشديا عضو SjSiUSj={  

اسلاید 7 :

اجتماع مجموعه ها...

 براي به دست آوردن اجتماع  S1,S2  

Øيکي از درختها زير درخت ديگري

Øفيلد والد يكي از ريشه ها را در ريشه ديگري قرار دهيم.

اسلاید 8 :

قانون وزن براي union(i,j)

تعريف :

Øاگر تعداد گره ها در درختي با ريشه i کمتر از تعداد گره هاي درختي با ريشه j باشد ، آنگاه j را والد i و در غيراين صورت i را والد j قرار مي دهيم .

اسلاید 9 :

پياده سازي قانون وزن براي union(i,j)...

Øبايد تعداد گره ها در هر درخت معلوم باشد

Øفيلد count

Øاگر i يک گره ريشه باشد، count[i] برابر تعداد گره ها در آن درخت مي باشد .

Øمي توانيم از فيلد parent ريشه براي نگهداري مقدار count  به صورت يک عدد منفي استفاده کنيم .

Øدر ابتدا فيلد parent  تمام گره ها برابر -1 است .

اسلاید 10 :

قضيه (به دست آوردن حداکثر عمق درخت ):

Øفرض کنيد که کارخود را با درختاني که هر کدام فقط يک گره دارند آغاز کنيم و T درختي با  m گره باشد که حاصل اجتماع با استفاده از تابع WeightedUnion است.

Øدر اين صورت عمق T حداکثر برابر [log2m]+1 خواهد بود