بخشی از مقاله
*** این فایل شامل تعدادی فرمول می باشد و در سایت قابل نمایش نیست ***
طراحي بهينه خرپاها با استفاده از نظريه آشوب
خلاصه
در بهينه سازي سازههاي خرپايي هدف معمولا کاهش هزينه هاي سازه در عين برآوردن محدوديتهاي طراحي نظير تنشهاي مجاز و تغيير شکلهاي گرهي است . براين اساس و با توجه به کاربردهاي گوناگون خرپاها، روشهاي متعددي براي بهينه سازي آنها ابداع شده است . در اين مقاله با معرفي يکي از جديدترين روشهاي بهينه سازي براساس نظريه آشوب (Chaos) که در ساير رشته هاي مهندسي و علوم کاربرد گستردهاي يافته است و تلفيق آن با روش گراديان وزن دار، سعي شده است از آن براي طراحي خرپاها با وزن کمينه استفاده شود. براي اين منظور الگوريتم ارائه شده بر روي سه خرپا با هندسه و قيدهاي متفاوت اعمال شده است . نتايج حاصل از طراحي خرپاها با اين روش نشان مي دهد که الگوريتم بهينه سازي ارائه شده، مي تواند به عنوان يک روش ساده و مناسب براي حل پارهاي از مسائل بهينه سازي در سازهها مورد استفاده قرار گيرد.
کلمات کليدي: بهينه سازي، خرپا، نظريه آشوب، روش گراديان وزندار، دنباله هاي آشوبناک
١. مقدمه
ويژگي هاي منحصر به فرد سازههاي خرپايي باعث توجه روز افزون معماران و طراحان براي استفاده از آنها در سازههاي جديد شده است . سازههاي خرپايي اگر براي پوشش دهانه هاي بزرگ استفاده شوند، داراي تعداد زيادي المان خواهند بود و اگر به عنوان دکلهاي انتقال نيرو به کار روند، معمولا به تعداد زيادي ساخته خواهند شد؛ بنابراين به نظر مي رسد با بهينه سازي اين نوع سازهها مي توان به ميزان قابل توجهي در منابع و هزينه ها صرفه جويي کرد.
طي سه دهه گذشته بررسي رفتار آشوبناک (chaotic) برخي از سيستم هاي ديناميکي توجه بسياري ازمجامع علمي را به خود جلب کرده است . اين گونه رفتار آشوبناک در زمينه هاي گوناگوني همچون مهندسي ، پزشکي ، زيست شناسي و اقتصاد مشاهده شده است . از لحاظ رياضي ، آشوب (chaos) به توانايي يک الگو و مدل ساده گفته مي شود که اگرچه اين الگو هيچ نشاني از پديدههاي تصادفي در خود ندارد، اما مي تواند منجر به ظهور رفتارهاي بسيار بي نظم در محيط شود. در حالت کلي مي توان گفت آشوب داراي سه مشخصه اصلي زير است [١] :
. وابستگي حساس به شرايط اوليه
. رفتار شبه تصادفي
. رفتار غيرتناوبي
با توجه به ويژگي هاي ياد شده، در حال حاضر تئوري آشوب به دو صورت در بهينه سازي مورد استفاده قرار مي گيرد [٢] :
. ترکيب ديناميک آشوبناک با شبکه هاي عصبي مصنوعي (CNN)
. استفاده از دنباله هاي آشوبناک براي تکامل متغيرها در الگوريتم هاي مختلف بهينه سازي (COA)
بررسي نتايج تجربي بدست آمده نشان مي دهد که استفاده از دنباله هاي آشوبناک براي توليد اعداد تصادفي در الگوريتم هاي بهينه سازي تصادفي (random-based optimization algorithms)، مزايايي نسبت به ساير روشها دارد [٣-٥].
در مقاله حاضر ابتدا به اختصار درباره روش گراديان وزن دار (Weighted Gradient Direction) توضيحاتي داده و سپس تلفيق آن با تئوري آشوب يا روش Weighted Gradient Direction Based Chaos Optimization Algorithms معرفي مي شود. در نهايت از اين روش براي طراحي بهينه خرپاها با وزن کمينه استفاده خواهد شد.
٢. روش گراديان وزن دار (WGD)
به طور کلي مي توان مسائل بهينه سازي را به صورت زير در نظر گرفت :
که در آن تابع هدف بوده و قيدهاي مساله مي باشد وX برابراست با . همچنين در اين روش فرض مي شود توابع در ديفرانسيل پذيرند. مساله غيرخطي مقيد (١) را مي توان به مساله غيرخطي زير، فقط با شرايط مرزي تبديل کرد:
که در آن تابع جريمه بوده و ضريب r مقدار عبارت جريمه را کنترل مي کند. مي توان نشان داد اگر r به اندازه مناسبي بزرگ باشد، جواب (٢) به جواب (١) همگرا خواهد شد.
حال فرض کنيم :
بنابراين اگر . باشد با حرکت x در جهت منفي گراديان تابع هدف مي توان به مقدار بهينه تابع هدف نزديک شد. همچنين قرار مي دهيم :
براي با حرکت در جهت مقدار کاهش يافته و شرط ارضا مي شود.
براساس اين تعاريف جهت گراديان وزن دار (weighted gradient direction) به صورت زير تعريف مي شود[٦] :
که در آن داريم :
در رابطه (٧)، .عدد صحيح مثبت بسيار کوچکي است . در نهايت از حرکت در جهت گراديان وزن دار بدست مي آيد که مي توان آن را به صورت رابطه (١٠) نوشت (انديس بالاي k مرحله حرکت به سمت نقطه بهينه را نشان مي دهد):
با توجه به معادلات ارائه شده مشاهده مي شود براي افزايش باعث افزايش مقدار wj خواهد شد. مسير مناسبي براي جستجوي مقدار بهينه تابع هدف است ، زيرا اگر باشد، در اين صورت است که در نتيجه جستجوي جواب در جهت منفي گراديان تابع هدف انجام مي گيرد و اگر ، مقادير بزرگ wj باعث جستجو در فضاي امکان پذير مي شود.
٣. تلفيق روش گراديان وزن دار با الگوريتم بهينه سازي آشوبناک (WGDCOA)
در بخش قبل روش WGD شرح داده شد. در اين قسمت با توجه به ويژگي هاي يادشده براي ديناميک آشوبناک، با استفاده از يک دنباله ، که رفتاري آشوبناک دارد، روش WGDCOA را معرفي ميکنيم . در بسياري از روشهاي COA از دنباله اي به نامLogistic Map براي توليد متغيرها استفاده مي شود. البته بررسي استفاده از ساير دنباله هاي آشوبناک در COA و تاثير آن در دقت و سرعت رسيدن به جواب درمرجع [١] آمده است . معادله Logistic به صورت زير تعريف مي شود:
در رابطه بالا پارامتر کنترل نام دارد. به ازاي به سادگي مي توان نشان داد که تمام ويژگي هاي يادشده براي يک ديناميک آشوبناک توسط اين دنباله توليد مي شود. شکل ١ نمودار تغييرات را برحسب k به ازاي نشان مي دهد.
نمودار بالا نشانگر رفتار شبه تصادفي اين دنباله مي باشد، در حالي که رابطه (١١) هيچ نشاني از متغيرهاي تصادفي در خود ندارد. با توجه به اين رفتار بي نظم ، يک دنباله آشوبناک با احتمال بسيار بالايي از يک مينيمم موضعي (local minimum) به مينيمم کلي (global minimum) همگرا مي شود [٧]. اساس بسياري از الگوريتم هاي بهينه سازي آشوبناک (COA) را مي توان به صورت زير خلاصه کرد:
١) فرض يک مقدار براي مشخص کردن تعداد مراحل جستجو و محاسبه ،که در آن داريم :
٢) محاسبه از رابطه (١١) و محاسبه متغير طراحي جديد، با استفاده از رابطه زير:
مراحل بالا تا زمان برقرار شدن شرط و اتمام مراحل جستجو ادامه مي يابد. در اين صورت مقدار بهينه تابع هدف خواهد بود.
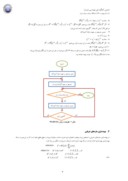
براي تلفيق اين روش با روش گراديان وزندار از الگوريتمي که توسط مرجع [٦] ارائه شده، استفاده مي کنيم . فلوچارت اين الگوريتم در شکل ٢ آورده شده است . مراحل مختلف اين الگوريتم به شرح زير مي باشد:
. اولين جستجو درجهت دنباله آشوبناک:
١) ورود وN(تعداد مراحل جستجو)
٢) محاسبه از رابطه (١٢)، از رابطه
٣) اگر باشد، در اين صورت قرار ميدهيم :
مراحل بالا بعد از N بار جستجو تا زماني که مقدار *P بهبود نيابد ادامه داده مي شود.
. جستجو در جهت گراديان وزن دار:
٥) محاسبه
٦) اگر قرار مي دهيم ، در غير اين صورت
مراحل بالا تا زماني که مقدار *P بهبود نيابد، ادامه داده مي شود.
. دومين جستجو در جهت دنباله آشوبناک :
٧) ورود
٨) محاسبه
٩) اگر باشد، در اين صورت قرار مي دهيم
١٠) قرار مي دهيم :