بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
مساله کوتاه ترین مسیربین تمامی زوج راس ها
تعریف مساله
الگوریتم Shortest Path Repeated
الگوریتم All-Pairs Ge eric Label-correcti g
مقایسه دوالگوریتم
اسلاید 2 :
تعریف مساله
در مساله کوتاه ترین مسیر بین زوج راس ها، فاصله کوتاه ترین مسیر بین هردو راس در شبکه تعیین می شود.
راه حل ها:
ü الگوریتم Shortest Path Repeated، این الگوریتم برای شبکه های خلوت (Sparse) مناسب است.
üالگوریتم All-Pairs Label-correcti g، این الگوریتم برای شبکه های متراکم (de se) مناسب است.
ü
اسلاید 3 :
فرض مساله
شبکه، قویاً همبند است.
در شبکه قویاً همبند، از هر گره به تمامی گره های دیگر یک مسیر جهت دار وجود دارد.
به راحتی می توانیم این شرط را برقرار کنیم.با انتخاب یک راس دلخواه (s)، و افزودن
یالهای (s, i) و (i , s ) با هزینه های به اندازه کافی بزرگ به ازای راسهای
iϵ - {s} (در صورتی که یال مربوطه نباشد)
شبکه شامل دور منفی نیست.
اسلاید 4 :
الگوریتم Shortest Path Repeated
حالت اول : شبکه شامل یال با طول منفی نیست.
در این حالت با باراجرای الگوریتم Si gle Shortest Path می توانیم مساله را حل کنیم. ( هر بار یکی از گره ها را به عنوان منبع انتخاب میکنیم.)
حالت دوم : شبکه شامل یال هایی با طول منفی است.
در این حالت، ابتدا شبکه را به یک شبکه با طول های غیر منفی تبدیل می کنیم. سپس الگوریتم Si gle Shortest Path را برای هر کدام از رئوس اجرا می کنیم.
اسلاید 5 :
الگوریتم Shortest Path Repeated
طریقه تبدیل شبکه به شبکه ای با طولهای غیرمنفی:
ابتدا یک گره را به عنوان گره مبدا(s) انتخاب می کنیم . سپس الگوریتم
FIFO Label Correcti g را اجرا می کنیم. در این صورت کم ترین فاصله از راس s تا همه رئوس دیگر محاسبه می شود.
با اجرای الگوریتم FIFO Label Correcti g
ü یا الگوریتم یک دور منفی را تشخیص می دهد. در این حالت مساله کوتاه ترین مسیر بین زوج راس ها جواب ندارد.
ü یا برای همه رئوس کوتاهترین مسیراز راسs را محاسبه می کند (d(j)). در این حالت برای هر یال، طول کاهش یافته را به صورت زیرمحاسبه می کنیم:
اسلاید 6 :
تبدیل شبکه به شبکه ای با طولهای غیرمنفی
شبکه با طول کاهش یافته را تشکیل می دهیم. در این حالت:
بنابراین شبکه به شبکه ای با طول های غیر منفی تبدیل شد.
در شبکه کاهش یافته الگوریتم Si gle Shortest Path را برای تا راس اجرا می کنیم.
درشبکه بدست آمده به مقدارکوتاه ترین فاصله بین دو راس lو k مقدار زیر را اضافه می کنیم تا مقدار واقعی کوتاه ترین فاصله در شبکه اولیه حاصل شود.
اسلاید 7 :
زمان اجرای الگوریتم
زمان تبدیل شبکه به شبکه با طول های غیر منفی :
ü زمان اجرای الگوریتم FIFO Label Correcti g : O(m )
زمان اجرای الگوریتم Si gle Shortest Path:
S( ,m,C)
با با اجرای Si gle Shortest Path :
O( * S( ,m, C))
زمان اجرای الگوریتم :
O( * S( ,m,C) = O(m * + * S( ,m, C))
اسلاید 8 :
قضیه
الگوریتم repeated shortest path کوتاه ترین مسیر بین زوج راس ها را در زمان O( * S( ,m,C) حل می کند.
اسلاید 9 :
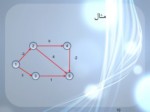
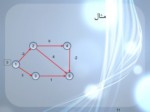
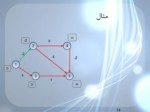
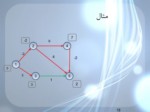
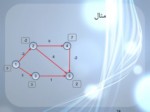
مثال
اسلاید 10 :
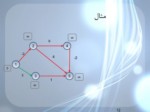
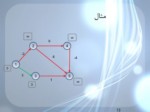
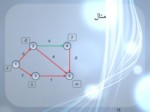
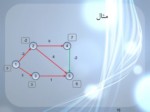
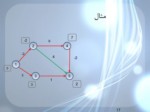
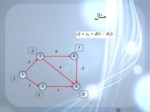
مثال