دانلود فایل پاورپوینت کار برد شبکه های عصبی در پردازش سریهای زمانی

بخشی از پاورپوینت

--- پاورپوینت شامل تصاویر میباشد ----

اسلاید 1 :

میانگین متحرک

• در آمار میانگین متحرک یکی از تکنیکهای مورد استفاده جهت تحلیل سریهای زمانی می باشد. این تکنیک جهت کم رنگ کردن نوسانات کوتاه مدت سری زمانی و نمایان کردن رفتار بلند مدت تر سری زمانی استفاده می شود.
• از لحاظ ریاضی میانگین متحرک مثالی از یک کانولوشن می باشد و از دیدگاه پردازش سیگنال به عنوان یک فیلتر قابل به کار گیری است. (در ادامه این موضوع را با جزئیات بیشتر بررسی می کنیم)

اسلاید 2 :

میانگین متحرک وزندار

• میانگین متحرک وزندار را می توان به صورت یک فیلتر گسسته در زمان به شکل زیر نمایش داد:
• بنا بر این پاسخ ضربه برابر خواهد بود با 

اسلاید 3 :

پاسخ فرکانسی

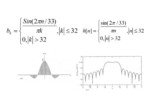
• پاسخ فرکانسی برابر خواهد بود با :
• در ادامه نمودار به لگاریتم دامنه این فیلتر را به ازای برخی مقادیر b مشاهده می کنیم.

اسلاید 4 :

• اثر فیلتر پایین گذر میانگین متحرک بر شاخص هفتگی بازار سهام داو جونز در یک دوره 10 ساله

الف)شاخص هفتگی

ب) میانگین متحرک 51 روزه  اعمال شده به الف

ج) میانگین متحرک 201 روزه

اسلاید 5 :

مدلهایی برای سریهای زمانی

• جهت پردازش سریهای زمانی لازم است که مدلی از این سریها داشته باشیم تا بتوانیم عملیاتی چون پیش بینی آینده سری و یا دسته بندی آن را بر اساس آن مدل انجام دهیم. در اینجا به معرفی سه مدل رایج برای این منظور می پردازیم:

–مدل Auto-regressive (AR)

–مدل Moving Average (MA)

–مدل ARMA که ترکیب دو مدل بالاست.

اسلاید 6 :

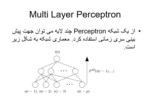
Auto-regressive Model

• در این مدل فرض می شود مقدار کنونی سری را می توان به صورت تابعی (خطی یا غیر خطی ) از پنجره ای از مقادیر گذشته سری به دست آورد:
• یا

اسلاید 7 :

• مدل خطی دارای دو محدودیت مهم است : اولا مستلزم فرض وجود رابطه حطی بین عناصر پیشین سری می باشند و ثانیا فرض می کنند سری Stationary می باشد.
• در مقابل با استفاده از مدل غیر خطی می توان تخمین دقیقتری از ویزگیهای سری زمانی مورد نظر به دست آورد. البته در صورت استفاده از مدل غیر خطی نیاز به نمونه های بیشتری در مرحله آموزش می باشد .

اسلاید 8 :

Moving Average

• می توان فرض کرد مقدار سری زمانی در یک مرحله را به صورت یک میانگین متحرک از نویزهای مراحل قبل قابل محاسبه است ، یعنی

اسلاید 9 :

Moving Average

• سوالی که مطرح می شود آن است که چگونه مقدار سری در یک نقطه که یک مقدار غیر تصادفی است را می توان با مجموع تعدادی متغیر تصادفی مدل کرد. در پاسخ می توان گفت همانطور که در معرفی Moving Average توضیح دادیم این عملگر به صورت یک فیلتر عمل می کند و با توجه به اینکه عموما نویز فرآیندی است که شامل طیف گسترده ای از فرکانسها می گردد ، بنابراین فیلتر میانگین متحرک می تواند از این طیف ، فرکانسهای مطلوب را گزینش کند تا یک سری زمانی غیر تصادفی حاصل شود.

اسلاید 10 :

ARMA Model

• همچنین می توان دو مدل قبلی را ترکیب کرده و مقدار سری در یک نقطه را بر اساس تابعی از مقادیر و نویزهای مراحل قبل بیان کرد ، یعنی