دانلود پاورپوینت داده‌کاوی جریان‌داده‌ها با درخت‌های تصمیم‌گیری

بخشی از پاورپوینت

اسلاید 1 :

کلاسه بندی

■ فرايندی دو مرحله ای است :

■ساخت مدل :

■تحليل يک مجموعه آموزشی که مجموعه‌ای از تاپل‌های پايگاه است و مشخص کردن برچسب کلاس‌های مربوط به اين تاپل‌ها .

■ يک تاپل X با يک بردار صفت X=(x1,x2,…,xn) نمايش داده می‌شود . فرض می شود که هر تاپل به يک کلاس از پيش تعريف شده متعلق است .

■هرکلاس با يک صفت که به آن صفت برچسب کلاس می‌گوييم مشخص می‌شود .

■ مجموعه آموزشی به صورت تصادفی از پايگاه انتخاب می شود .

■به اين مرحله ، مرحله يادگيری نيز می گويند .

■استفاده از مدل :

■از طريق يک تابع y=f(X) برچسب  کلاس هر تاپل X از پايگاه را پيش بينی می شود .

■اين تابع به صورت قواعد کلاسه‌بندی ، درخت‌های تصميم گيری يا فرمول‌های رياضی است .

اسلاید 2 :

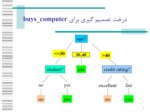
درخت های تصميم گيری

■يکی از روش های کارآمد و با کاربرد گسترده کلاسه بندی است .

■مدل حاصل از اين روش به صورت درختهای تصميم گيری است :

■هر گره در اين درخت نشان دهنده يک آزمون بر روی يک صفت است .

■هر شاخه خارج شونده از يک گره نشان دهنده خروجی های ممکن آزمون است .

■هر برگ نشان دهنده يک برچسب کلاس است .

■نحوه استفاده از درخت تصميم گيری :

■اگر تاپلی چون X که برچسب کلاس آن نامشخص است داشته باشيم صفات اين تاپل در درخت مورد آزمون قرار می گيرند و يک مسير از ريشه به سمت يک برگ که برچسب يک کلاس را دارد ايجاد می شود .

اسلاید 3 :

الگوريتم برای درخت های تصميم گيری

■الگوريتم پايه

■درخت به صورت بالا-پايين بازگشتی ساخته می شود .

■در آغاز تمام مجموعه آموزشی در ريشه قرار دارند .

■فرض می کنيم صفات مقادير گسسته دارند .

■صفات به صورت بازگشتی بر حسب صفات انتخاب شده بخش بندی می شوند .

■صفات آزمون بر اساس يک روال هيوريستيک مانند بهره اطلاعاتی ، شاخص جينی يا نسبت بهره انتخاب می شوند .

■شرايط توقف الگوريتم

■تمام نمونه های مربوط به يک نود متعلق به يک کلاس باشند .

■صفتی برای بخش بندی بيشتر باقی نمانده باشد .

■نمونه ای باقی نمانده باشد .

اسلاید 4 :

چالش ها

■روش های ساختن درختان تصميم گيری فرض می کنند که تمام مجموعه آموزشی به طور همزمان می تواند در ديسک ذخيره شود .

■روش های مذکور بصورت پياپی مجموعه آموزشی را از ديسک می خوانند .

■هدف : طراحی درخت های تصميم گيری که هر نمونه آموزشی را فقط يکبار بخواند زمان کوتاه ثابتی را برای پردازش آن صرف کند .

اسلاید 5 :

نکات کليدی

■برای يافتن بهترين صفت در هر گره ، در نظر گرفتن يک زيرمجموعه کوچک از نمونه های آموزشی که از آن گره عبور می کنند کافی است .

■با در دست داشتن جريانی از نمونه ها ، اولين نمونه ها برای انتخاب صفت ريشه استفاده می شوند .

■با تعيين شدن صفت ريشه ، نمونه های بعدی به سمت پايين و برگهای مربوطه عبور داده می شوند تا برای انتخاب صفت در آنجا استفاده شوند .

■اين عمل به صورت بازگشتی تکرار می شود .

■چه تعداد نمونه در هر گره لازم است ؟

■از يک نتيجه آماری به نام Hoeffding bound  استفاده می کنيم .

اسلاید 6 :

Hoeffding Bound

■يک متغيير تصادفی با نام r که دارای مقادير حقيقی و برد R است را در نظر بگيريد .

■فرض کنيد که n مشاهده مستقل از اين متغير انجام می‌دهيم .

■ميانگين اين مشاهدات :

■Hoeffding Bound نشان می‌دهد که ميانگين واقعی متغير r  بعد از اين n مشاهده با احتمال 1-δ حداقل برابر –ε       است که در آن : 

اسلاید 7 :

چه تعداد نمونه کافی است ؟

■فرض کنيد G(Xi)  روال ابتکاری برای انتخاب صفات آزمون باشد مانند بهره اطلاعاتی و شاخص جينی .

■فرض کنيد که Xa  صفت دارای بالاترين مقدار ارزيابی بعد از n نمونه باشد .

■فرض کنيد که Xb صفت دارای دومين بالاترين مقدار ارزيابی بعد از n نمونه باشد .

■آنگاه با يک δ مناسب اگر  بعد از مشاهده n نمونه :                                            آنگاه :

■گره می تواند بر حسب Xa شکافته شود و نمونه های بعدی به سمت برگهای جديد عبور داده می شوند .

■

■

اسلاید 8 :

درختان تصميم گيری بسيار سريع VFDT

■برابری‌‌ها :

■وقتی که دو يا بيشتر صفت در G بسيار شبيه هستند نمونه‌های زيادی برای تصميم‌گيری بين آنها ، با اطمينان بالا نياز است .

■در اين مورد ، اينکه چه صفتی انتخاب می شود اختلاف اندکی را بوجود می‌آورد .VFDT  بصورت انتخابی تصميم می‌گيرد که يک برابری وجود دارد و شکاف را روی يکی از بهترين صفت‌های جاری انجام می‌دهد .

■محاسبه G  :

■بخش قابل توجهی از زمان به ازای هر نمونه برای محاسبه G صرف می شود .

■محاسبه دوباره G برای هر نمونه جديد ناکارا است ، چون احتمال تصميم برای شکاف در آن نقطه مشخص غير محتمل است .

■ بنابراين VFDT به کاربر اجازه می‌دهد تا يک حداقل تعداد برای نمونه های جديد يا nmin  را مشخص کند که بايد در هر برگ انباشته شود قبل از اينکه G دوباره محاسبه شود .

اسلاید 9 :

درختان تصميم گيری بسيار سريع VFDT

■ حافظه :

■بسياری از برنامه های کاربردی RAM محدودی برای يادگيری مدلهای پيچيده دارند .

■حافظه مورد استفاده VFDT همان حافظه مورد نياز برای نگهداری شمارنده‌ها در برگهای در حال رشد است .

■اگر به حداکثر حافظه برسيم VFDT برگهايی را که احتمال شکاف در آنها کم است غيرفعال می کند تا حافظه برای برگهای جديد فراهم شود .   

■هنگامی که احتمال شکاف يک برگ غيرفعال از برگهای موجود  بيشتر شود آن برگ دوباره می‌تواند فعال شود .