دانلود پاورپوینت مدارهای مرتبه اول

بخشی از پاورپوینت

اسلاید 1 :

  مدار مرتبه اول چيست؟

nهر مداري كه شامل تنها يك عنصر ذخيره كنندة انرژي، تعدادي منبع و تعدادي مقاومت باشد مدار مرتبه اول ناميده مي‌شود.

nعنصر ذخيره‌كنندة انرژي مي‌تواند خازن يا مقاومت باشد.

nيكي از خواص مدارهاي مرتبه اول اينست كه پاسخ مدار داراي تابع ديفرانسيلي درجه اول مي‌باشد.

اسلاید 2 :

  مفاهيم مربوط به مدارهاي درجه اول

nمعادلة ديفرانسيل و ويژگي‌ها و روشهاي حل آن.

nپاسخ طبيعي.

nثابت زماني.

nپاسخ گذرا و پاسخ ماندگار مدار.

اسلاید 3 :

  انواع مدارهاي مرتبه اول

nبطور كلي دو نوع مدار مرتبه اول وجود دارد:

nمدار RC: مدارهايي كه داراي مجموعه‌اي از مقاومتها و منابع هستند و تنها يك خازن نيز در آنها وجود دارد.

nمدار RL: مدارهايي كه داراي مجموعه‌اي از مقاومتها و منابع هستند و تنها يك سلف نيز در آنها وجود دارد.

اسلاید 4 :

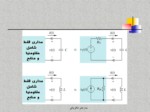
nهمانگونه كه در مبحث مدارهاي معادل نورتن و تونن گفته شد، هر مدار شامل منابع و مقاومتها را مي‌توان بصورت تركيب سري يك منبع ولتاژ و مقاومت (معادل تونن) يا تركيب موازي يك منبع جريان و مقاومت (معادل نورتن) نمايش داد.

اسلاید 5 :

nهمانگونه كه ديده مي‌شود معادلات ديفرانسيل بدست آمده درجه اول هستند. براي حل اين معادله مي‌توان از روشهاي حل معادلات ديفرانسيل يا از روش لاپلاس استفاده كرد.

nبراي حل معادلات ديفرانسيل نياز به دانستن شرايط اوليه است. شرايط اوليه با توجه به شكل مدار معلوم مي‌شوند.

اسلاید 6 :

  تعيين شرايط اولية مدار RC

nيكي از ويژگي‌هاي خازن اينست كه ولتاژ آن بطور ناگهاني تغيير نمي‌كند.

nدر شكل زير يك مدار RC نشان داده شده است كه سوئيچ آن درست در زمان صفر بسته مي‌شود و خازن شروع به شارژ مي‌كند.

اسلاید 7 :

nولتاژ منبع مقدارثابتي است و مشتق آن برابر با صفر مي‌باشد. بنابراين:

n

n

n

n

nيكي از جوابهاي معادله فوق مي‌تواند بفرم ke-1000t باشد.

nبا توجه به صورت مسأله مقدار ولتاژ اولية خازن برابر با صفر است و چون ولتاژ خازن تغيير ناگهاني ندارد، مقدار آن بلافاصله بعد از صفر نيز برابر با صفر خواهد ماند.

nبا جايگزيني شرايط فوق در معادله مقدار k بدست مي‌آيد.

اسلاید 8 :

nاز آنجا كه بلافاصله بعد از بستن كليد، ولتاژ خازن برابر با صفر است:

n

Vs=R i0+ + Vc(0+)

100=105 i0+ + 0

i0+=10-3

اسلاید 9 :

يا به عبارت ديگر شرط اوليه مسأله به اينصورت است:

i0+=10-3

 با جايگذاري شرط اوليه در فرمول بدست آمده خواهيم داشت:

i(t)=10-3 e-1000t

اسلاید 10 :

  روش دوم حل مدارهاي RC

nدر قسمتهاي قبلي با استفاده از روشهاي حل معادلات ديفرانسيل و يا لاپلاس پاسخ مدار محاسبه مي‌شد. روش ديگري نيز براي يافتن پاسخ مدارهاي Rc وجود دارد.

nابتدا با استفاده از مقاومت معادل، ثابت زماني مداربدست مي‌آيد:

n

nسپس از فرمول زير استفاده مي شود:

e-t/RC*(مقدار نهايي-مقدار اوليه)+مقدار نهايي=پاسخ مدار