بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
Dr. H. Bolandi
These are also gi en by the eigen alues of matrix A. Notice that the system is open loop stable. This means that with no control action δ, if an initial disturbance is introduced in the angle θ, it will go back to zero asymptotically. As the metacentric height :
gets closer to zero, one open loop pole goes to zero. (Can you see this from the form of the A matrix?What is the physical significance of a zero pole?) The open loop zero is the root of the numerator of the transfer function is −0.2742 .The transfer function can also be computed by starting with the equations of motion :
اسلاید 2 :
« كنترلپذيري و مشاهدهپذيري»
به طور كلي تحليلهاي به عمل آمده در خصوص يك سيستم شامل تحليلهاي كمي و تحليلهاي كيفي است. در تحليلهاي كمي به دنبال آن هستيم تا دريابيم كه exactsolution يك سيستم نسبت به يك ورودي اعمالي چيست؟
اين موضوعي بوده كه تاكنون به آن پرداختهايم. در بحث تحليلهاي كيفي به دنبال خواص سيستم يا مشخصات عمومي سيستم هستيم. در اين راستا در بررسي و تحليل كيفي سيستمها دو خاصيت كنترلپذيري و مشاهدهپذيري براي سيستمهاي خطي را در اينجا مورد بررسي قرار ميدهيم.
كالمن نشان داد كه يك حذف قطب ـ صفر تنها به ناپايداري سيستم منجر شده، كه عليالظاهر سيستم ميتواند از يك تابع تبديل پايدار نيز برخوردار باشد.در چنين حالتي تابع تبديل درجهاي كمتر از درجة سيستم خواهد داشت و مددهاي ناپايدار يا از ورودي سيستم تأثير نميگيرند (كنترلناپذير) و يا اينكه اين مدها در خروجي ظاهر نميشوند. (مشاهدهناپذير)
اسلاید 3 :
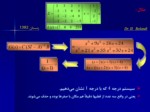
بعبارتي كالمن نشان ميدهد كه هر سيستم بصورت زير
را ميتوان با 4 زير سيستم نشان داد :
اسلاید 4 :
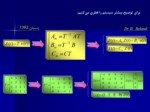
جمعبندي :
اگر يك سيستم SISO داشته باشيم و درجه تابع تبديل آن كمتر از بعد سيستم باشد آنگاه سيستم داراي خصوصيات زير است:
يا سيستم كنترلپذير نيست.
يا سيستم مشاهدهپذير نيست.
يا سيستم نه كنترلپذير نه مشاهده پذير است.
پايدار پذيري: سيستمهايي هستند كه زيرسيستم كنترلناپذير آنها پايدار باشد.
آشكارپذيري:سيستمهايي هستند كه زيرسيستم رؤيت ناپذير آنها پايدار باشند.
اسلاید 5 :
دلائل كنترل ناپذيري / مشاهده ناپذيري
علاوه بر مباحث تحقق ناپذيري اين گونه سيستمها ميتوان به دلايل زير اشاره نمود:
كنترلناپذيري
تعريف متغير حالت اضافي در سيستم
وجود تقارن زياد در سيستم
وجود فقط نيروهاي داخلي
مشاهدهناپذيري
هر وقت كه امكان اندازهگيري حالتسيستم وجود نداشته باشد.
اسلاید 6 :
از اينرو اگر رتبة ماتريس :
باشد آنگاه n بردار L.T در اين ماتريس وجود خواهد داشت از آنجا كه n بردار L.I فضاي حالت n بعدي را ميپوشاند لذا سيستم را بطور كامل كنترلپذير حالت ميگوئيم .
در اينجا ميتوان موضوع را به دو طريق زير ادامه داد:
اسلاید 7 :
This is full rank, 3. Therefore, the system is controllable and we can change any state θ, w, or q using the dive planes at will. Note, however, that some changes may be impractical or even impossible in practice; for example, even if the system is controllable it is not feasible to change the pitch angle to, say, 90 degrees! This would require an enormous dive plane strength which is not available in practice.
اسلاید 8 :
زيرفضاي كنترلپذير
ميدانيم كه زيرفضاي كنترلپذير سيستم داده شده با معادله فوق زيرفضاي خطي تشكيل شده از حالتهايي است كه ميتوان آنها را در يك زمان محدود به هر حالت نهايي انتقال داد. (حالتهاي كنترلپذير) . در اينجا يك تبديل همانندي حالت كه سيستم را به فرم كانونيكي نمايش ميدهد را به نحوي پيدا ميكنيم كه توسط آن تحليل خواص كنترلپذيري سيستم به وضوح نمايش داده خواهند شد.
اسلاید 9 :
از آنجا كه B قسمتي از ماتريس كنترلپذيري حالت است ستونهاي B تماماً در زير فضاي كنترلپذير حالت قرار دارند.
اسلاید 10 :
شايان توجه است كه اگر سيستمي داراي مقادير ويژه مجزا باشد آنگاه ميتوان نشان داد كه زير فضاي كنترلپذير حالت سيستم توسط بردارهاي ويژه متناظر با قطبهاي كنترلپذير سيستم پوشانده ميشود يعني اينكه امكان دارد كه تعريف كنيم كه :
مثال : در سيستم زير اولاً تحقيق كنيد كه سيستم به طور كامل كنترلپذير حالت است يا خير؟ ثانياً در صورتي كه سيستم بطور كامل كنترلپذير حالت نباشد زيرفضاي كنترلپذير و ناپذير آن را تعيين كنيد.