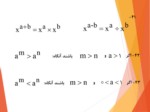بخشی از پاورپوینت
اسلاید 1 :
85 -برای بدست آوردن تعداد مقسوم علیه های طبیعی یک عدد به صورت زیر عمل می کنیم .ابتدا عدد را به عوامل اول تجزیه می کنیم . سپس به توان هر عامل یک واحد اضافه کرده توانها ی بدست آمده را در هم ضرب می کنیم . مثال عدد 2400
تعداد مقسوم علیه های اول هرعدد برابر است با تعداد پایه های اول آن عدد مثال:2400 سه مقسوم علیه اول دارد
تعداد مقسوم علیه های مرکب برابر است با:
(1 +تعداد مقسوم علیه های اول )-تعداد مقسوم علیه های طبیعی
تعداد مقسوم علیه های زوج برابر است با :
به توان تمام عوامل اول آن عدد یک واحد اضافه میکنیم غیر از توان روی2 سپس اعداد بدست آمده را در هم ضرب می کنیم.
تعداد مقسوم علیه های مضرب 3 برابر است با :
به توان تمام عوامل اول آن عدد یک واحد اضافه میکنیم غیر از توان روی3 سپس اعداد بدست آمده را در هم ضرب می کنیم.
اسلاید 2 :
94- معادلۀ ax=bرا در نظر می گیریم:
1- اگر باشد معادله فقط یک جواب دارد و جواب آن است.
2- اگر و باشند معادله جواب ندارد و آنرا معادلۀ غیرممکن می نامند.
3- اگر و باشند معادله بیشمار جواب دارد و آنرا معادلۀ مبهم می نامند.
اسلاید 3 :
معادله خط
97- معادلۀ کلی خطوطی که از مبدأ مختصات می گذرند و شیبشان aاست. به صورت y=ax می باشد.
98- معادلۀ کلی خطوطی که شیبشان a بوده و محور عرض را در نقطه ای به عرض bقطع می کنند بصورت y=ax+bمی باشد.
99- شیب، عرض از مبدا و طول از مبدا خط y=ax+b به ترتیب a، b و
می باشند.
اسلاید 4 :
100-کلیۀ خطوطی که شیبشان مساوی و عرض از مبداءشان مختلف باشند با هم موازیند.
101-کلیۀ خطوطی که شیبشان مساوی و عرض از مبداءشان نیز برابر باشند بر هم منطبقند.
102-کلیۀ خطوطی که عرض از مبداء شان مساوی باشد در نقطه ای واقع بر محور عرض یکدیگر را قطع می کنند.
103-کلیۀ خطوطی که طول از مبداء شان مساوی باشند. در نقطه ای واقع بر محور طول یکدیگر را قطع می کنند.
104-معادلۀ عمومی خطوطی که موازی محور طول می باشند به صورت y=bاست.
اسلاید 5 :
105- معادلۀ محور طول به صورت است.
106- معادلۀ عمومی خطوطی که موازی محور عرض میباشند به صورت است.
107- معادلۀ محور عرض به صورت می باشد.
108- معادلۀ خطی که طول از مبداء و عرض از مبداء آن p و q باشد به صورت
است.
اسلاید 6 :
110- در معادلۀ :
1) اگر A و B و C مخالف صفر باشند، خط در نقاطی غیر از مبداء محورها را قطع می کند.
2) اگر و و باشند، خط از مبداء مختصات می گذرد.
3) اگر و باشند، خط موازی محور عرض یا منطبق برآن است.
4) اگر و باشند، خط موازی محور طول یا منطبق بر آن است.
اسلاید 7 :
138- خط مماس در نقطۀ تماس بر شعاع دایره عمود است.
139- دو دایره نسبت به هم سه حالت دارند:
1) دو دایره یکدیگر را در دو نقطه قطع می کنند. در این صورت طول خط
المرکزین از مجموع دو شعاع کوچکتر و از تفاضل دو شعاع بزرگتر است.
2)دو دایره بر هم مماسند.
الف) مماس داخلی: در این صورت طول خط المرکزین با تفاضل دو شعاع مساوی است.
ب) مماس خارجی: در این صورت طول خط المرکزین
با مجموع دو شعاع مساوی است.
اسلاید 8 :
140- دو دایره هیچ نقطۀ مشترکی ندارند.
الف) متداخل: در این صورت طول خط المرکزین ازتفاضل دو شعاع کوچکتر است.
ب) متخارج در این صورت طول خط المرکزین از مجموع دو شعاع بزرگتر است.
141- طول دو مماسی که از نقطۀ واقع در خارج دایره، بر آن دایره رسم می شوند برابرند.
اسلاید 9 :
142- دایره محاطی یک چند ضلعی، دایره ای است که بر اضلاع چند ضلعی مماس است.
143- دایره محیطی یک چند ضلعی، دایره ای است که از رئوس چند ضلعی می گذرد.
144- مرکز دایره محاطی هر مثلث محل تلاقی نیمساز زوایای مثلث است و شعاع دایره محاطی برابر فاصلۀ مرکز دایره تا هر ضلع مثلث
می باشد.
اسلاید 10 :
145- مرکز دایره محیطی هر مثلث محل تلاقی عمود منصفهای اضلاع مثلث است و شعاع دایره محیطی برابر فاصلۀ مرکز تا رئوس مثلث
می باشد.
146- مرکز دایره محاطی و مرکز دایرۀ محیطی مثلث متساوی الاضلاع بر هم منطبقند.
147- شعاع دایرۀ محیطی مثلث متساوی الاضلاع دو برابر شعاع دایرۀ محاطی آن مثلث است.
148- مساحت هر n ضلعی منتظم برابر است با: