بخشی از پاورپوینت
--- پاورپوینت شامل تصاویر میباشد ----
اسلاید 1 :
پارهخط در هندسه به جزئی از خط گفته میشود که به دو نقطه انتهایی محدود شده، و تمامی نقاط مابین آندو را در بر بگیرد.
در مورد چندضلعیها، پارهخط را ضلع مینامند هرگاه که دو نقطهٔ انتهایی آن در حکم دو رأس مجاور چندضلعی باشد، و در غیر این صورت، به آن قطر گفته میشود.
اگر AوB دو نقطه انتهایی پاره خطی باشند این پاره خط را با نماد AB نشان میدهیم.
اسلاید 2 :
برخی نکات در رابطه با زاویه ها
. اگر دو زاویه مجاور باشند ، زاویه ای که بین نمیسازهای این دو زاویه تشکیل می شود ، نصف کل زاویه است
اسلاید 3 :
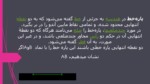
. نیمسازهای دو زاویه مجانب بر هم عمودند.
. دو زاویه متقابل به رأس با هم مساویند.
اسلاید 4 :
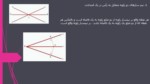
٤. نیم سازهای دو زاویه متقابل به رأس در یک امتدادند.
. هر نقطه واقع بر نیمساز زاویه از دو ضلع زاویه به یک فاصله است و بالعکس هر نقطه که از دو ضلع یک زاویه به یک فاصله باشد ، بر نیمساز زاویه واقع است.
اسلاید 5 :
قارن یا همامونی به معنای تشابه بخشها حول محور یا مرکز تقارن است[۱]. این واژه در هنرهای گوناگون به ویژه هنرهای تجسمی و در علومی مانند فیزیک بسیار کاربرد دارد.
در علوم، به طور مطلق ناوردایی نسبت به تبدیلات هندسی را تقارن گویند مفهوم تقارن به مفاهیمی چون تقارن در زمان (ناوردایی تحت تبدیل هندسی انتقال در مولفه صفرم چاربردار مکان) نیز تعمیم داده میشود
اسلاید 6 :
مثلث
می دانید که هر مثلث دارای اجزایی می باشد
الف) اجزای اصلی: به سه زاویه و سه ضلع هر مثلث اجزای اصلی آن می گویند.
ب) اجزای فرعی: میانه ، ارتفاع ، نیمساز ، عمود منصف ، قاعده و ... اجزای فرعی مثلث هستند.
ارتفاع:
خطی که از یک رأس بر ضلع مقابل یا امتداد آن عمود می شود. (AH ارتفاع)
اسلاید 7 :
تساوی مثلث ها:
دو مثلث که بر هم منطبق شوند و کاملاً یکدیگر را بپوشانند با هم مساوی هستند. ما با داشتن فقط سه جزء از اجزای اصلی دو مثلث می توانیم ثابت کنیم که دو مثلث با هم برابرند. این سه جزء اصلی باید به صورت زیر باشد:
حالت اول: دو ضلع و زاویه بین آن ها (ض ز ض)
حالت دوم: دو زاویه و ضلع بین آن ها (ز ض ز)
حالت سوم: سه ضلع مساوی (ض ض ض)