بخشی از مقاله
كاربرد آمار در علم باستان شناسي
چكيده:
بايد پذيرفت كه درجه علمي بودن هر تخصصي به ميزان بهره گيري آن علم از رياضيات به خصوص آمار بستگي دارد.
تا سال 1950 ميلادي پژوهشگران باستان شناسي اغلب به روش هاي سنتي گرايش داشتند و استفاده از علوم رياضي وطبيعي به طور كلي در پژوهش هاي آنان نقشي نداشت كه در اين ميان كشف پروفسور ليبي (Libby) در زمينه تاريخگذاري به روش كربن 14 نشان داد كه باستان شناسان براي يافته ها و تفسير داده هاي خود مي بايست به علوم ديگر نيز
بپردازند. همواره تحليل مواد فرهنگي، طبقه بندي و نامگذاري از جمله موضوعات مورد توجه پژوهشگران باستان شناسي مي باشد. در اين مقاله، هدف نه تدوين تاريخچه اين فعاليت ها بلكه ارائه و معرفي روش ها و طرح هاي پژوهشي آماري در حوزه باستان شناسي است وتلاش شده است تا الگوهاي لازم براي پياده كردن موارد مشابه براي طبقه بندي و نامگذاري مواد فرهنگي آماده گردد. مواد فرهنگي كه در اين مقاله بدان خواهيم پرداخت از محوطه كوكوبوداي ژاپن (Kokobudai) جمع آوري، طبقه بندي و مورد مطالعه قرار گرفته است و به دوران كهن سنگي تعلق دارد.
مقدمه
با مراجعه به كتابها، مقاله ها و طرح هاي پژوهشي باستان شناسان نشان مي دهد كه در زمينه كاربرد آمار و رياضيات در علم باستان شناسي به ندرت گامي برداشته شده است، در حالي كه همواره استقرار، تحليل و تفسير مواد فرهنگي، طبقه بندي و نامگذاري از جمله موضوعات مورد توجه آنها بوده است.
باستان شناسان سنتي از طريق مقايسه شكل دست سازها به طبقه بندي و تاريخگذاري مواد فرهنگي مي پردازند ولي تجربه ثابت كرده است كه چشم باستان شناسي ابزار دقيقي براي انجام چنين كاري نيست و وجه تمايزهاي بسيار كوچك همواره از ديد آنها پوشيده مانده است و اينجاست كه روش هاي آماري در طبقه بندي و نامگذاري مواد اهميت پيدا مي كنند.
در طبقه بندي دست سازها دو عامل مورد تأكيد مي باشد: 1- تكنيك و ساخت 2- شكل يا فرم
شكل يا فرم دست سازها هدف اصلي طبقه بندي به كمك روش هاي آماري را شامل مي شود زيرا مي دانيم از ديدگاه رياضي و آمار هر شكل اندازه ونسبت هاي خاص خود را دارد كه اين اندازه ها و نسبت ها به مانند شناسنامه آنرا از ديگر نمونه ها متمايز مي سازد و شاخص خوبي براي شناخت و معرفي آن نمونه قلمداد مي گردد.
در مقاله حاضر سعي گرديده است كه با ارائه و معرفي روش هاي آماري، باستان شناسان در كنار ديگر متخصصان بتوانند با استفاده از ابزار پژوهش هاي مشترك توانايي لازم براي كسب دانش هاي نوين را بدست آورند و بتوانند گام هايي براي تفسيرو نتيجه گيري از داده ها و مشاهدات و يافته هاي بدست آمده خود بردارند و با طرح مسائل پژوهشي و كاربرد آمار در علم باستان شناسي كوشش شده است تا الگوهاي لازم براي پياده كردن موارد مشابه براي طبقه بندي مواد فرهنگي آماده شود.
جمع آوري، اندازه گيري ومحاسبات آماري مواد فرهنگي
مواد فرهنگي كه در اين مقاله بدان خواهيم پرداخت از محوطه كوكوبوداي ژاپن (Kokobudai) جمع آوري، طبقه بندي ومورد مطالعه قرار گرفته است.
30 نمونه كارد مانند (شامل كاردهاي كولدار) تشكيل يك مجموعه را داده اند. اندازه گيري ها يا صفات موردنظر در طرح شماره 1 نشان داده شده است.
براي هر يك كاردها پنج صفت اندازه گيري شده است كه توضيح چگونگي اين اندازه ها به شرح زير مي باشد:
1) L طول نمونه
2) (نسبت عرض نمونه به طول)
3) (نسبت بيشترين ضخامت نمونه به عرض آن)
4) (نسبت عرض نمونه در طول از انتهاي ابزار)
5) (نسبت ضخامت ابزار در طول از نوك ابزار به طول نمونه)
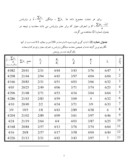
اندازه گيري اصلي و اوليه نمونه بدست آمده در جدول شماره (1) آورده شده است.
اين اندازه ها در عدد 100 ضرب و عدد 1/0 به آن افزوده و لگاريتم نپرين (طبيعي) گرفته شده و براي انجام عمليات رياضي و آماري مهيا گرديده است.
جدول شماره 1: اندازه گيري اوليه و اصلي 30 نمونه كارد از محوطه كوكوبوداي ژاپن (Kokobudai)
رديف L طول
1 6/5 /43 /31 /85 /10
2 4/2 /57 /53 /86 /19
3 5/6 /39 /56 /91 /10
4 5/2 /42 /41 /58 12/
5 6/3 /38 /64 /93 /15
6 5/6 /55 /40 /99 /17
7 5/7 /50 /41 /77 /09
8 4/1 /80 /18 /84 /06
9 6/4 /53 /37 /60 /18
10 5/2 /48 /56 /82 /14
11 7/7 /42 /43 /62 /13
12 6/3 /57 /36 /65 /13
13 8/1 /53 /31 /83 /10
14 4/4 /36 /23 /87 /10
15 3/9 /51 /56 /83 /14
16 5/2 /34 /58 1/05 /14
17 4/3 /46 /52 /58 /16
18 6/3 /55 /36 /70 /11
19 7/6 /44 /35 /80 /11
20 5/8 /48 /53 /61 /11
21 4/3 /62 /45 /53 /11
22 6/9 /29 /63 1 /15
23 5/3 /47 /43 /43 /14
24 6/8 /51 /54 /65 /27
25 6/7 /38 /57 1/18 /15
26 5/5 /36 /49 1/03 /15
27 5/9 /54 /29 /49 /14
28 4/3 /58 /40 74/ /16
29 4/4 /48 /43 /74 /20
30 5 /49 /39 /78 /13
بجز صفت اول يعني طول نمونه كه اندازه گيري ساده اي است كه مستقيماً از ابزار بدست آمده است.بقيه صفات را آقايان رو (Roe 1964)، گراهام (Graham 1970) و هودسون (Hodson 1971) پيشنهاد و مورد تأكيد قرار داده اند.
براي هر صفت مجموع داده ها ، ميانگين و واريانس و انحراف معيار كه برابر جذر واريانس مي باشد محاسبه و نتيجه در جدول شماره (2) مشاهده مي گردد.
جدول شماره (2) : اندازه گيري ثانويه نمونه (اندازه ها در 100 ضرب بعلاوه 1/0 شده است از آنها لگاريتم نپرين گرفته شده) و همچنين محاسبه ميانگين، واريانس و انحراف معيار براي هركدام صفات بكارگرفته شده در پژوهش
رديف L
جمع
ميانگين هر رديف
1 6/47 3/76 3/43 4/44 2/31 20/41 4/082
2 6/04 4/04 3/97 4/45 2/94 21/44 4/298
3 6/32 3/66 4/03 4/51 2/31 20/83 4/166
4 6/25 3/74 3/71 4/06 2/49 20/25 4/05
5 6/64 3/64 4/16 4/53 2/71 21/48 4/296
6 6/32 4 3/69 4/59 2/83 21/43 4/286
7 6/33 3/9 3/71 4/34 2/2 20/49 4/10
8 6 4/38 2/89 4/43 1/8 19/5 3/9
9 6/46 3/97 3/61 4/09 2/89 21/02 4/204
10 6/25 3/87 4/03 4/4 2/64 21/19 4/24
11 6/64 3/74 3/76 4/13 2/57 20/84 4/168
12 6/44 4/04 3/58 4/17 2/57 20/8 4/16
13 7 3/97 3/43 4/42 2/31 21/13 4/226
14 6/08 3/58 3/13 4/46 2/31 19/56 3/912
15 5/97 3/93 4/03 4/42 2/64 20/99 4/198
16 6/25 3/52 4/06 4/65 2/64 21/12 4/224
17 6/06 3/83 3/95 4/06 2/77 20/67 4/134
18 6/44 4 3/58 4/24 2/4 20/66 4/132
19 6/63 3/78 3/55 4/38 2/4 20/74 4/148
20 6/36 3/87 3/97 4/11 2/4 20/71 4/142
21 6/06 4/12 3/8 3/97 2/4 20/35 4/07
22 6/53 3/37 4/14 4/6 2/71 21/35 4/27
23 6/27 3/85 3/76 3/76 2/64 20/28 4/056
24 6/52 3/93 3/99 4/17 3/29 21/9 4/38
25 6/5 3/64 4/04 4/77 2/71 21/66 4/332
26 6/3 3/58 3/89 4/63 2/71 21/11 4/222
27 6/38 4 3/37 3/89 2/64 20/28 4/056
28 6/06 4/06 3/69 4/3 2/77 20/88 4/176
29 6/08 3/87 3/76 4/3 3 21/01 4/202
30 6/21 3/89 3/66 4/35 2/57 20/68 4/136
مجموع كل
همبستگي وارتباط بين صفات
براي بررسي و ميزان ارتباط و همبستگي بين صفات مورد بحث ابتدا طبق شرح ذيل ضريب همبستگي r را محاسبه نموده و اگر r=1 باشد گوئيم همبستگي بين دو صفت كامل و مستقيم است و اگر r=-1 باشد رابطه بين دو صفت كامل و معكوس واگر r=0 بدست آيد گوئيم بين دو صفت همبستگي و ارتباطي وجود ندارد. پس همواره مي باشد و مثبت بودن r نشان مي دهد كه يك رابطه مستقيم و منفي بودن نشان مي دهد كه رابطه معكوس بين دو صفت وجود دارد و هر چقدرr به 1 يا 1- نزديكر شود همبستگي قويتر و اگر r به صفر نزديكتر شود همبستگي ضعيف خواهد بود.
اگر دو صفت x و y از واحدهاي اندازه گيري تبعيت نمايند همبستگي را مي توان از ضريب همبستگي پيرسن طبق فرمول كه و مي باشند بدست مي آيد.
براي اينكه r از واحدهاي اندازه گيري تبعيت نكند مقاديرx و y را طبق فرمول هاي و استاندارد مي كنيم و در اين حالت معادله خط رگرسيون y=ax+b بصورت تبديل وبنابراين مقدار r از فرمول كه و انحراف معيار x و y مي باشند بدست مي آيد.
دراين پژوهش مقدار ضريب همبستگي r بين صفات مورد بحث را از فرمول فوق محاسبه و در جدول (3) آورده ايم و براي مشخص شدن نحوه محاسبه، بطور نمونه محاسبه ضريب همبستگي بين دوصفت L و را با استفاده از داده هاي جدول (2) آورده ايم.
كه اين مقدار نشان مي دهد كه يك رابطه و همبستگي مستقيم و قوي بين دو صفت L و وجود دارد.
يا به عنوان مثال ديگر رابطه بين دوصفت و را مشاهده مي نمائيد.
r = 0/82 نشان مي دهد كه يك رابطه مستقيم و قوي بين دو صفت B/L و B1/B2 وجود دارد. كه ضريب همبستگي بين صفات به كار گرفته شده در پروژه بهمين ترتيب محاسبه و نتيجه در جدول زيرآورده شده است.
جدول شماره (3) محاسبه ضريب همبستگي r بين صفات به كارگرفته شده در اين پژوهش
صفات L
L 1 0/755 0/355 0/620 0/269
0/755 1 0/465 0/82 0/356
0/355 0/465 1 0/565 0/766
0/620 0/82 0/565 1 0/433
0/269 0/356 0/766 0/433 1
با مراجعه به جدول شماره (3) كه ضريب همبستگي بين صفات بكارگرفته شده در اين پژوهش را نشان مي دهد درمي يابيم كه روابط مستقيمي بين صفات مورد بررسي 30 نمونه كارد موجود است واعداد بدست آمده ميزان و درجه همبستگي را بين صفات به نمايش مي گذارد.
حال با استفاده از جدول آناليز واريانس و آزمون F (فيشر) مي خواهيم پاسخ به اين سئوال را بپردازيم كه آيا مي توان 30 نمونه كارد را از ديدگاه شكل طبقه بندي نمود؟يا خير؟
آزمون F
براي آزمون اينكه آيا مجموعه مورد مطالعه تمايز واختلاف معني داري وجود دارد و اينكه آيا مي توان تمامي نمونه ها را در يك گروه قرار داد؟ يا خير؟
بدين منظور ابتدا F محاسبه شده را به كمك جدول آناليز واريانس به صورت زير بدست مي آوريم.
منبع تغييرات مجموع مجذورات SS درجه آزادي df ميانگين مجذورات MS F محاسبه شده
بين گروهها
k-1
داخل گروهها
N-k
كلT
N-1
SSها از فرمول هاي زير بدست مي آيند:
پس از محاسبه SSها جدول آناليز واريانس را تشكيل مي دهيم و از آنجا F محاسبه شده بدست مي آيد و آنرا با جدول با درجه آزادي N-k و N-1 مقايسه مي كنيم (F جدول در پايان هر كتاب آماري وجود دارد) اگر F محاسبه شده از كمتر باشد مي توان نتيجه گرفت كه در مجموعه مورد مطالعه اختلاف معني داري وجود ندارد ومي توان تمام نمونه ها را در يك گروه قرار داد در غيراينصورت تصميم مي گيريم كه امكان گروه بندي جامعه مورد مطالعه وجود دارد.
طبق داده هاي جدول شماره (2) مجموعه مورد پژوهش داريم:
جدول شماره 5 : نتيجه محاسبات انجام يافته (جدول آناليز واريانس)
منبع تغييرات SSها d.f MS محاسبهF
بين گروهها
k-1=30-1=29
داخل گروهها
N-n=120
كل T
N-1=150-1=149
كه با مقايسه مقدار بدست آمده F=2/61 با و جدول در مي يابيم كه امكان گروه بندي مجموعه مورد پژوهش وجود دارد.
گروه بندي مجموعه مورد پژوهش
هدف از گروه بندي جامعه مورد مطالعه يافتن تمايزها بين يك مجموعه از آثار فرهنگي به نام «كارد» مي باشد ومي خواهيم نمونه ها را طوري كنار دهيم كه ميزان تمايز آنها به حداقل برسد كه براي انجام اين كار از كميت L.S.D* «كوچكترين تفاوت معني داري» استفاده مي كنيم كه از فرمول زير بدست مي آيد:
كه در مجموعه مورد پژوهش طبق نتايجي كه قبلاً در جدول آناليز واريانس بدست آورده ايم ، و t از جدول t استودنت برابر بدست مي آيد. پس داريم:
سپس ميانگين 30 نمونه كارد را كه براي 5 صفت محاسبه و در جدول (2) آورده ايم برحسب نزولي مرتب مي كنيم و براي سهولت در انجام محاسبات ميانگين ها را در 10 ضرب و بطور نزولي مرتب كرده و نتيجه را در جدول (4) مشاهده مي نمائيد.
جدول (4) تنظيم نزولي ميانگين 30 نمونه كارد
شماره نمونه 24 25 5 2 6 22 10 13 16 26
43/8 43/32 42/96 42/88 42/86 42/7 42/4 42/26 42/24 42/22
شماره نمونه 9 29 15 28 11 3 12 19 20 30
42/04 42/02 41/76 41/76 41/68 41/66 41/6 41/48 41/42 41/36
شماره نمونه 17 18 7 1 21 27 23 4 14 8
41/34 41/32 41 40/82 40/7 40/56 40/56 40/5 39/12 39
بعداز مرتب شدن ميانگين ها، مقدار L.S.D را از بزرگترين ميانگين كسر مي كنيم.
هرميانگين كه از نتيجه بدست آمده بزرگتر و يا مساوي باشد در يك گروه قرار مي گيرد و سپس عمليات را براي تعيين گروه هاي بعدي تكرار مي كنيم.